-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
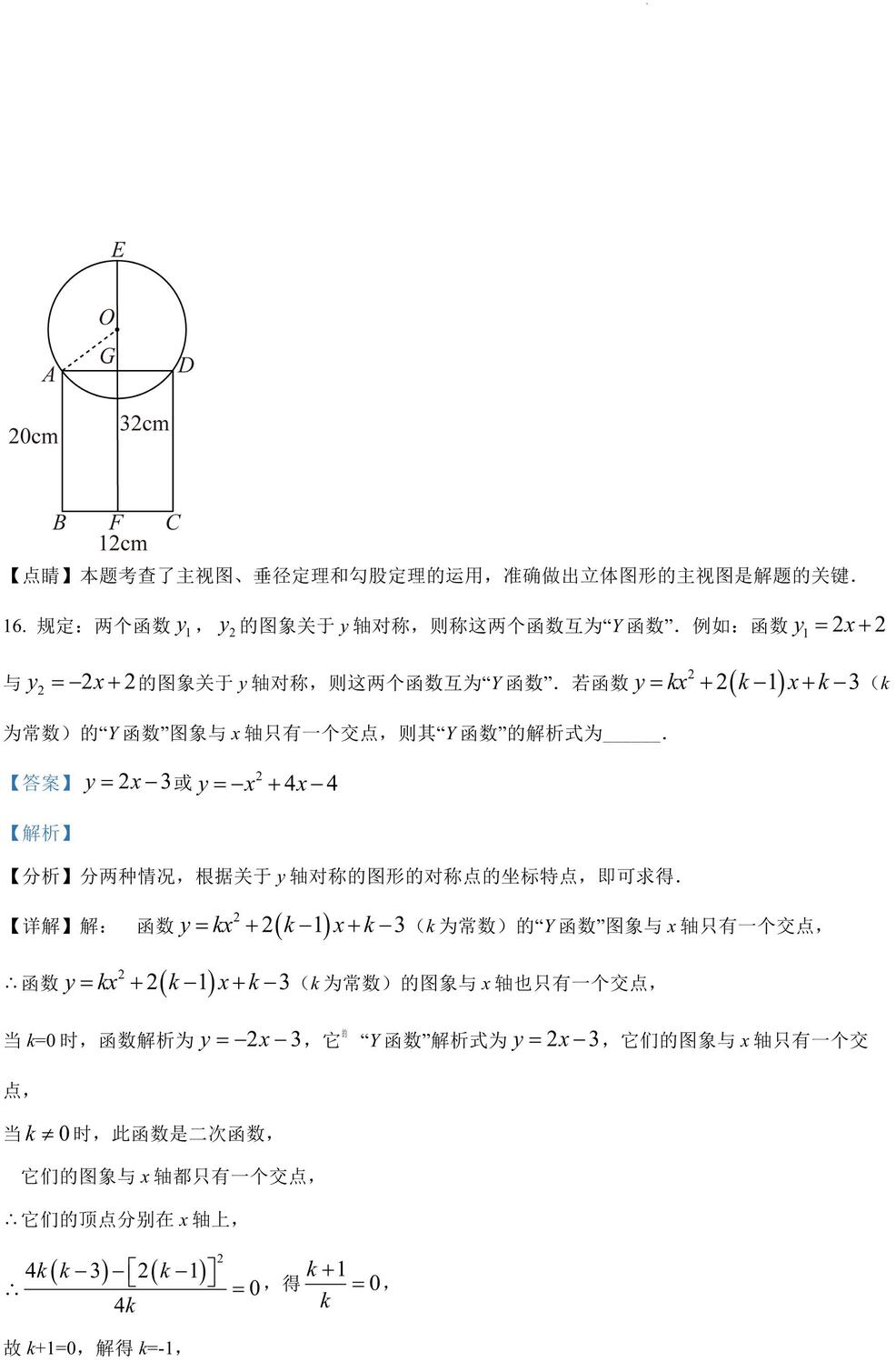
【点睛】本题考查了主视图、垂径定理和勾股定理的运用，准确做出立体图形的主视图是解题的关键．
16. 规定：两个函数 1y ， 2y 的图象关于 y 轴对称，则称这两个函数互为“Y 函数”．例如：函数 1 2 2y x= +与 2 2 2y x= - + 的图象关于 y 轴对称，则这两个函数互为“Y 函数”．若函数 ( )2 2 1 3y kx k x k= + - + - （k为常数）的“Y 函数”图象与 x 轴只有一个交点，则其“Y 函数”的解析式为______．
【答案】 2 3y x= - 或 2 4 4y x x= - + -
【分析】分两种情况，根据关于 y 轴对称的图形的对称点的坐标特点，即可求得．
【详解】解： 函数 ( )2 2 1 3y kx k x k= + - + - （k 为常数）的“Y 函数”图象与 x 轴只有一个交点，
函数 ( )2 2 1 3y kx k x k= + - + - （k 为常数）的图象与 x 轴也只有一个交点， 当 k=0 时，函数解析为 2 3y x= - - ，它 “Y 函数”解析式为 2 3y x= - ，它们的图象与 x 轴只有一个交点， 当 0k ? 时，此函数是二次函数， 它们的图象与 x 轴都只有一个交点，
它们的顶点分别在 x 轴上，
- - -é ù? ? = ，得故 k+1=0，解得 k=-1，