-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
即 DC×CE=OC×PC， 设 CE=x，则 DE=6+x，OE=3+ ，OC=3+ -x=3- ，PC=4+x， 整理得：x2+10x-24=0， 解得：x=2(负值已舍)．
∴CE 的长为 2．
【点睛】本题考查了切线的性质，相似三角形的判定和性质，圆周角定理，解题的关键是学会利用参数构建方程解决问题．
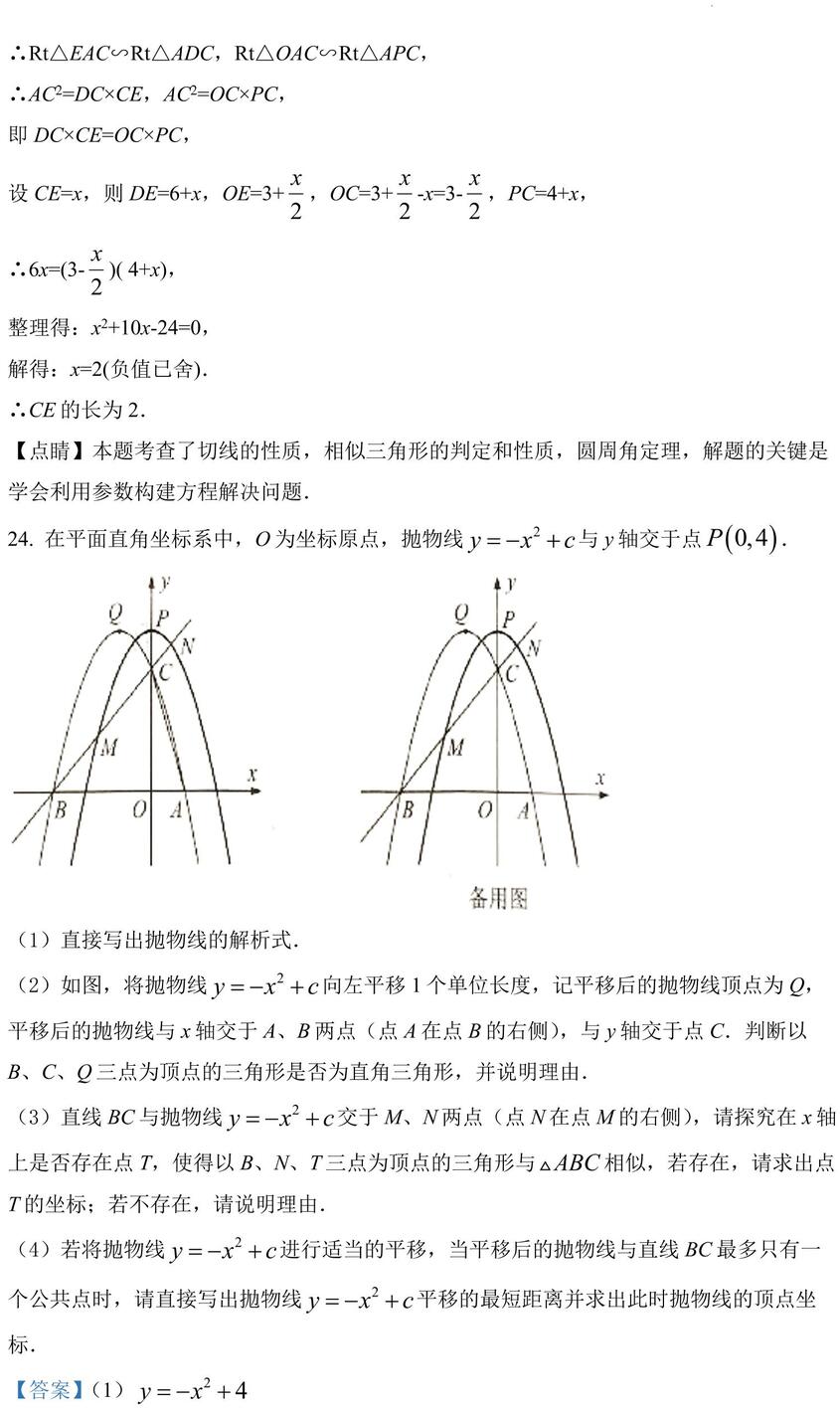
24. 在平面直角坐标系中，O 为坐标原点，抛物线 与 y 轴交于点 ．
（1）直接写出抛物线的解析式．
（2）如图，将抛物线 向左平移 1 个单位长度，记平移后的抛物线顶点为 Q，平移后的抛物线与 x 轴交于 A、B 两点（点 A 在点 B 的右侧），与 y 轴交于点 C．判断以
B、C、Q 三点为顶点的三角形是否为直角三角形，并说明理由．
（3）直线 BC 与抛物线 交于 M、N 两点（点 N 在点 M 的右侧），请探究在 x 轴上是否存在点 T，使得以 B、N、T 三点为顶点的三角形与 相似，若存在，请求出点
T 的坐标；若不存在，请说明理由．
（4）若将抛物线 进行适当的平移，当平移后的抛物线与直线 BC 最多只有一个公共点时，请直接写出拋物线 平移的最短距离并求出此时抛物线的顶点坐标．
【答案】（1）