如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
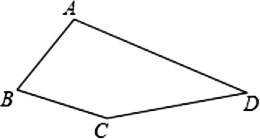
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE²=BE²+CE²,求点E运动路径的长度.
如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.

(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE²=BE²+CE²,求点E运动路径的长度.
解答过程见word版
如图,在△ABC中,BC=4,点D、E分别为AB、AC的中点,则DE=【 】
如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.
如图,已知∠AOX=30°,OA=2,AB⊥OA,AB=OA,则B的坐标为________.
在长方形ABCD中,长为4,宽为2,N为CD的中点,M在AD上,且MBC=BMN,求AM.
如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=【 】
如图,在四边形ABCD中,AC与BD相交于点O, ∠ABC=∠DAC=90°,tan∠ACB=1/2,BO/OD=4/3,则S△ABD/S△CBD =________.