已知△ABC是直角三角形,∠B=90°,AB=3,BC=5,AE=2√5,连接CE,以CE为底作直角三角形CDE,CD=DE. F是AE边上的一点,连接BD,BF,∠FBD=45°,则AF长为________.
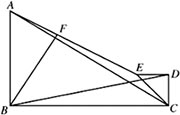
已知△ABC是直角三角形,∠B=90°,AB=3,BC=5,AE=2√5,连接CE,以CE为底作直角三角形CDE,CD=DE. F是AE边上的一点,连接BD,BF,∠FBD=45°,则AF长为________.

3√5/4
如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.
如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF【 】
如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.
如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是【 】
已知:如图,E、F在AC上,AD//CB且AD=CB,∠D=∠B.求证:AE=CF.
如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.(1)求证:△AOC≌△BOD;(2)若AD=1,BD=2,求CD的长.
如图,已知∠AOX=30°,OA=2,AB⊥OA,AB=OA,则B的坐标为________.
如图,有一张一个角为 30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是【 】
小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为 60°,求山高【 】
在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=________.
如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
如图,在RtΔABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为_______.
如图,ΔABC中,点E在边AC上,EB=EA,∠A=2∠CBE,CD垂直于BE的延长线于点D,BD=8,AC=11,则边BC的长为_______.