如图,在△ABC中,AB=AC,tanB=3/4,点D为BC上一动点,连接AD,将△ABD沿AD翻折得到△ADE,DE交AC于点G,GE<DG,且AG:CG=3:1,则S△AGE/S△ADG =________.
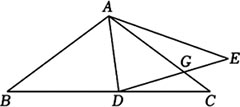
如图,在△ABC中,AB=AC,tanB=3/4,点D为BC上一动点,连接AD,将△ABD沿AD翻折得到△ADE,DE交AC于点G,GE<DG,且AG:CG=3:1,则S△AGE/S△ADG =________.

49/75(解答过程见word版)
在Rt△ABC中,∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F,且AF=4,EF=√2,则AC=________.
如图,每个小正方形边长均为1,则图中的三角形(阴影部分)与下图中△ABC相似的是【 】
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为【 】
已知ΔABC的周长为16,点D,E,F分别为ΔABC三条边的中点,则ΔDEF的周长为【 】
如图,BC//DE,且BC<DE,AD=BC=4,AB+DE=10,则AE/AC的值为__________.
如图,在ΔABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为_________.
泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】
如图,在△ABC中,BC=4,点D、E分别为AB、AC的中点,则DE=【 】
如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.
如图,已知∠AOX=30°,OA=2,AB⊥OA,AB=OA,则B的坐标为________.
在长方形ABCD中,长为4,宽为2,N为CD的中点,M在AD上,且MBC=BMN,求AM.
如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为【 】
已知三角形两边的长分别是4和10,则此三角形第三边的长可能是【 】
如图,在△ABC中,AB=AC,∠ABC=72°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.