-
关注“蜜蜂引路”，分配平台账号.
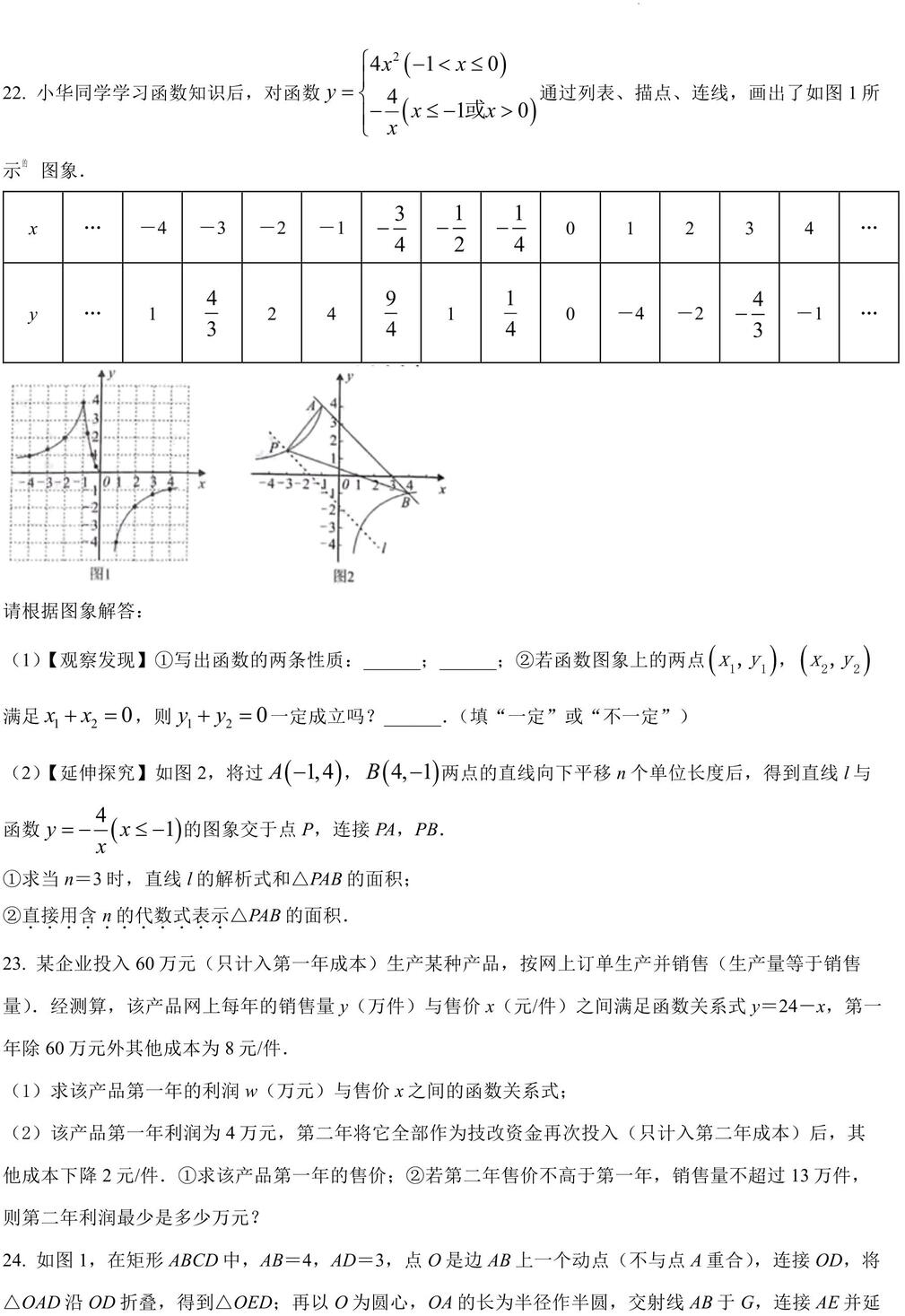
22. 小华同学学习函数知识后，对函数通过列表、描点、连线，画出了如图 1 所示 图象． 请根据图象解答：
（1）【观察发现】①写出函数的两条性质：______；______；②若函数图象上的两点 ( )1 1,x y ， ( )2 2,x y满足 1 2 0x x+ = ，则 1 2 0y y+ = 一定成立吗？______．（填“一定”或“不一定”）
（2）【延伸探究】如图 2，将过 ( )1,4A - ， ( )4, 1B - 两点的直线向下平移 n 个单位长度后，得到直线 l 与函数 ( )4 1y x
= - ? - 的图象交于点 P，连接 PA，PB．
①求当 n＝3 时，直线 l 的解析式和△PAB 的面积；
②直接用含．．．．n．的代数式表示．．．．．．△PAB 的面积．
23. 某企业投入 60 万元（只计入第一年成本）生产某种产品，按网上订单生产并销售（生产量等于销售量）．经测算，该产品网上每年的销售量 y（万件）与售价 x（元/件）之间满足函数关系式 y＝24－x，第一年除 60 万元外其他成本为 8 元/件．
（1）求该产品第一年的利润 w（万元）与售价 x 之间的函数关系式；
（2）该产品第一年利润为 4 万元，第二年将它全部作为技改资金再次投入（只计入第二年成本）后，其他成本下降 2 元/件．①求该产品第一年的售价；②若第二年售价不高于第一年，销售量不超过 13 万件，则第二年利润最少是多少万元？
24. 如图 1，在矩形 ABCD 中，AB＝4，AD＝3，点 O 是边 AB 上一个动点（不与点 A 重合），连接 OD，将
△OAD 沿 OD 折叠，得到△OED；再以 O 为圆心，OA 的长为半径作半圆，交射线 AB 于 G，连接 AE 并延