用同样的小正方体拼搭成右图甲、乙两个几何模型这两个几何模型的表面积【 】。
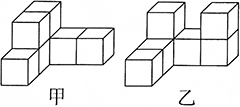
A、甲 > 乙
B、甲 = 乙
C、甲 < 乙
D、不好比较
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
①4+5/4>5，②59×1.01<60，③5/9÷9/19>1，其中判断正确的是【 】。
如图，把1L水倒入甲容器中，水深8cm，倒入乙容器中，水深12cm，则甲容器的底面积与乙容器的底面积比是________。说说你是怎么想的?
用小棒摆正六边形(如图)，摆10个正六边形需要____根小棒;摆n个正六边形需要__________根小棒。
下图方格纸每个方格的边长是1cm，线段ON绕O点顺时针旋转90°，则N点旋转后位置的数对是___,___;线段ON扫过图形的面积是______cm2.
23AA是一个四位数(相同字母表示相同的数字)。如果这个四位数既是2的倍数，也是3的倍数，则这个四位数可能是______;如果这个四位数既是3的倍数也是5的倍数，则这个四位数是______.
一件商品打八五折销售，“八五折”表示原价的______%，如果这件商品的原价是m元，这件商品的实际售价是______元。
右图是一个正方体的表面展开图，各面都标有数字，则数字“-4”对面的数是“_____”。
在图中的几何体是由棱长为 1 厘米的小正方体拼搭成的，它的表面积是______平方厘米，至少还需要______个这样的小正方体，才能拼搭成棱长为 3 厘米的一个正方体。
将图中的纸片沿虚线折起来，可做成一个正方体，则这个正方体的A面对面是字母______.
用三个同样的小正方体拼成一个长方体，表面积减少1平方分米，每个小正方体的表面积是________。
小亮同学分别用8个1cm³的正方体测量了4个盒子的容积(如下图)第【 】个盒子的容积最大。
一个正方体木块，6个面都涂上红色，然后把它切成大小相等的27小正方体(如下图)，其中有三个面是红色的小立方体有【 】个。
如图，瓶底的面积和锥形杯口的面积相等，将瓶子中的液体倒入锥形杯子中，能倒满【】杯。
一个棱长为4分米的正方体钢锭，把它锻造成底面积为32平方分米的圆锥体，高是多少分米？
一个圆锥和一个圆柱等底等高，它们的体积之和是 36 立方分米，圆柱的体积比圆锥的大_____立方分米。
一个圆锥形的沙堆，底面周长是 18.84 米，高是 2 米，用这堆沙铺在一条宽 10 米的公路上，铺 5 厘米厚，这堆沙能铺多长的公路？
一个立体图形，从上面看到的形状是，从左面看到的形状是。搭这样的一个几何体，最少需要_____个小立方块，最多需要_____个小立方块。
下图扇形的半径是 r 。请你想象，用这个扇形围成一个高为 h 的圆锥（接缝处不计） , 圆锥的高 h 与扇形半径 r 之间的关系是【 】。