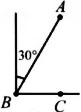
如图,海中有一小岛A,在B点测得小岛A在北偏东30°方向上,渔船从B点出发由西向东航行10n mile到达C点,在C点测得小岛A恰好在正北方向上,此时渔船与小岛A的距离为【 】n mile.
A、10√3/3
B、20√3/3
C、20
D、10√3
如图,海中有一小岛A,在B点测得小岛A在北偏东30°方向上,渔船从B点出发由西向东航行10n mile到达C点,在C点测得小岛A恰好在正北方向上,此时渔船与小岛A的距离为【 】n mile.

A、10√3/3
B、20√3/3
C、20
D、10√3
D
【解析】
在直角三角形ABC中,∠A=30°,BC=10,
∴AC=√3 BC=10√3.
如图,抛物线y=ax²+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为【 】
某蓄电池的电压为48V,使用此电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为I=48/R.当R=12Ω时,I的值为______A.
已知一次函数y=kx+b的图像经过点(0,1)与点(2,5),求该一次函数的表达式.
在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是【 】
点(1,y1 ),(2,y2 ),(3,y3 ),(4,y4)在反比例函数y=4/x图像上,则y1,y2,y3,y4中最小的是【 】
水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长 C与r的关系式为C=2πr下列判断正确的是【 】
如下左图,在Rt△ABC中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中BP长与运动时间t(单位:s)的关系如右图,则AC的长为【 】