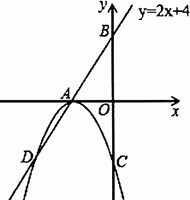
如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,-4).
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为 E,与y 轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则△EFG的面积与△ACD的面积是否存在8倍的关系?若有请直接写出F点的坐标.
如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,-4).

(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为 E,与y 轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则△EFG的面积与△ACD的面积是否存在8倍的关系?若有请直接写出F点的坐标.
(1)根据题意,直线AB的解析式为y=2x+4,令x=0,得y=4;令y=0,得x=-2,∴A(-2,0),B(0,4).根据A为抛物线的顶点,设抛物线的方程为y=a(x+2)²,将点C(0,-4)代入上式,可得a=-1,∴抛物线的方程为:y=-(x+2)².(2)设点E在平移过程中的坐标为(m,2m+4),则平移后抛物线的解析式为:y=-(x-m)²+2m+4,∴F(0,-m²+2m+4).①∵E为抛物线的顶点,∴∠BEF≥90°,若△BEF∼△BAO,则∠BEF=90°,∴OA/EF=OB/BE,即2/EF=4/BE,可得BE=2EF.如图,过点E作EH⊥y轴于点H,则H的坐标为:H(0,2m+4),∴BH=|2m|,FH=|m² |.在Rt△BEF中,由射影定理得:BE²=BH⋅BF,EF²=FH⋅BF,∵BE=2EF,∴BH=4FH,即|2m|=4|m² |,若2m=-4m²,解得m=-1/2或m=0(与点B重合,舍去);若2m=4m²,解得m=1/2或m=0(与点B重合,舍去),此时点E位于第一象限,∠BEF为锐...
查看完整答案已知BD 垂直平分AC,∠BCD=∠ADF,AF⊥AC.(1)证明四边形ABDF是平行四边形;(2)若AF=DF=5,AD=6,求AC的长.
先化简,再求值:(3x/(x-2)-x/(x+2))÷x/(x²-4),在-2,0,1,2四个数中选一个合适的代入求值.
计算:√12-2tan60°+(√2014-1)0-(1/3)-1
如图,下列图形是将正三角形按一定规律排列,则第5个图形中所有正三角形的个数有______.
如图,双曲线y=k/x经过Rt△OBC斜边上的点A,且满足AO/AB=2/3,与BC交于点D,S△BOD=21,则k=________.
如图所示,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为_________.
如图,在平面直角坐标系中,ΔOAB的顶点A,B的坐标分别为(3,),(4,0).把ΔOAB沿x轴向右平移得到ΔCDE,如果点D的坐标为(6,),则点E的坐标为_________.
在半面直角坐标系中,点(3,2)关于x轴对称的点的坐标为【 】
若关于x的一元二次方程x2+2x-k=0无实数根,则k的取值范围是_________.
如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是【 】