关注蜜蜂引路，注册平台账号.
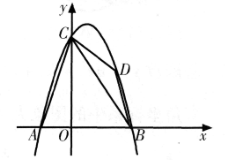
如图所示，抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点，与y轴交于点C，且点A的坐标为A(-2,0)，点C的坐标为C(0,6)，对称轴为直线x=1.点D是抛物线上一个动点，设点D的横坐标为m(1<m<4)，连接AC，BC，DC，DB.
（1）求抛物线的函数表达式；
（2）当ΔBCD的面积等于ΔAOC的面积的3/4时，求m的值；
（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B,D,M,N为顶点的四边形是平行四边形.若存在，请直接写出点M的坐标；若不存在，请说明理由.
（1）由题意得，解得故抛物线的函数表达式为y=-3/4x2+3/2x+6（2）过点D作DE⊥x轴于点E，交BC于点G，过点C作CF⊥ED交ED的延长线于点F.∵点A的坐标为(-2,0)，∴OA=2∵点C的坐标为(0,6)∴OC=6∴S_ΔAOC=1/2 OA⋅OC=1/2×2×6=6∴S_ΔBCD=3/4 S_ΔAOC=3/4×6=9/2当y=0时，-3/4x2+3/2x+6=0，解得x1=-2，x2=4.∴B(4,0)设直线BC的函数表达式为y=kx+n则，解得，∴直线BC的函数表达式为y=-3/2x+6.则点D的坐标为D(m,- 3/4m2+3/2m+6)，点G的坐标为G(m,-3/2 m+6)，∴ DG=- 3/4m2+3/2m+6-(-3/2m+6)= - 3/4m2+3m∵点B的坐标为(4,0)，∴OB=4.∴SΔBCD=SΔCDG+SΔBDG=1/2 DG⋅CF+1/2 DG⋅BE=1/2 DG(CF+BE)=1/2 DG⋅BO=1/2×(-3/4 m2+3m)×4=-3/2 m2+6m.则有- 3/2m2+6m=9/2解得m1=1（不合题意，舍去），m2=3.∴m的值为3.（3...
查看完整答案如图，双曲线y=k/x经过Rt△OBC斜边上的点A,且满足AO/AB=2/3，与BC交于点D,S△BOD=21，则k=________.
已知点A(x1,y1 )，B(x2,y2 )，C(x3,y3 )都在反比例函数y=k/x (k<0)的图像上，且x1<x2<0<x3，则y1，y2，y3的大小关系是【】
如图所示,点P(3a,a)是反比例函数y=k/x(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 】
如图，双曲线y=k/x(k>0)与⊙O在第一象限内交于P、Q两点，分别过P、Q两点向x轴和y轴作垂线，已知点P坐标为(1，3)，则图中阴影部分的面积为________.
如图，已知在Rt△ABC中，∠ACB=90°,AC=1,AB=2,则sinB的值是______.