为了解甲、乙两座城市的邮政企业4月份收入的情况,从这两座城市的邮政企业中,各随机抽取了25家邮政企业,获得了它们4月份收入(单位:百万元)的数据,并对数据进行整理、描述和分析,下面给出了部分信息:
a.甲城市邮政企业4月份收入的数据的频数分布直方图如下:
数据分成5组:6≤x<8,8≤x<10,10≤x<12,12≤x<14,14≤x≤16.
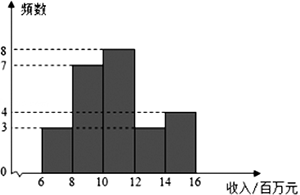
b.甲城市邮政企业4月份收入的数据在10≤x<12,这一组的数据是:
10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8.
c.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下:
平均数 中位数
甲城市 10.8 m
乙城市 11.0 11.5
根据以上信息,回答下列问题:
(1).写出表中m的值:
(2).在甲城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为p1,在乙城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为p2.比较p1,p2的大小,并说明理由:
(3).若乙城市共有200家邮政企业,估计乙城市的邮政企业4月份的总收入(直接写出结果).

