初中数学-中考试题(山东省枣庄市 2020年统计计算)

问答题（2020年山东省枣庄市）

2020年，新型冠状病毒肆虐全球，疫情期间学生在家进行网课学习和锻炼，学习和身体健康状况都有一定的影响．为了解学生身体健康状况，某校对学生进行立定跳远水平测试．随机抽取50名学生进行测试，并把测试成绩（单位：m）绘制成不完整的频数分布表和频数分布直方图．

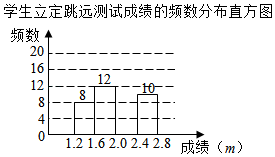
学生立定跳远测试成绩的频数分布表

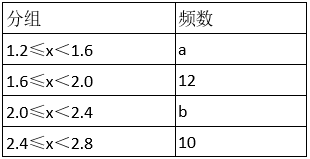
请根据图表中所提供的信息，完成下列问题：

（1）表中a＝_______，b＝_______；

（2）样本成绩的中位数落在_______范围内；

（3）请把频数分布直方图补充完整；

（4）该校共有1200名学生，估计该学校学生立定跳远成绩在2.4≤x＜2.8范围内的有多少人？

答案解析

（1）由统计图得，a＝8，b＝50﹣8﹣12﹣10＝20，故答案为：8，20；（2）由中位数的意义可得，50个数据从小到大排列处在中间位置的两个数在2.0≤x＜2.4组内，故答案为：2.0≤x＜2.4...

查看完整答案

讨论

初中数学

欧拉（Euler，1707年～1783年）为世界著名的数学家、自然科学家，他在数学、物理、建筑、航海等领域都做出了杰出的贡献．他对多面体做过研究，发现多面体的顶点数V（Vertex）、棱数E（Edge）、面数F（Flatsurface）之间存在一定的数量关系，给出了著名的欧拉公式．（1）观察下列多面体，并把下表补充完整：（2）分析表中的数据，你能发现V、E、F之间有什么关系吗？请写出关系式：__________．

解不等式组并求它的所有整数解的和．

各顶点都在方格纸的格点（横竖格子线的交错点）上的多边形称为格点多边形，它的面积S可用公式S＝a+1/2b﹣1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克（Pick）定理”．如图给出了一个格点五边形，则该五边形的面积S＝_______．

如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF的周长是_______．

人字梯为现代家庭常用的工具（如图）．若AB，AC的长都为2m，当α＝50°时，人字梯顶端离地面的高度AD是_______m．（结果精确到0.1m，参考依据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

如图，AB是⊙O的直径，PA切⊙O于点A，线段PO交⊙O于点C．连接BC，若∠P＝36°，则∠B＝_______．

已知关于x的一元二次方程(a﹣1)x2﹣2x+a2﹣1＝0有一个根为x＝0，则a＝_______．

若a+b＝3，a2+b2＝7，则ab＝_______．

如图，已知抛物线y＝ax2+bx+c的对称轴为直线x＝1．给出下列结论：①ac＜0；②b2﹣4ac＞0；③2a﹣b＝0；④a﹣b+c＝0．其中，正确的结论有【】

如图，在矩形纸片ABCD中，AB＝3，点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC＝∠ECA，则AC的长是【】

统计初步

垃圾的分类回收不仅能够减少环境污染、美化家园，甚至能够变废为宝、节约资源。为增强学生垃圾分类意识，推动垃圾分类进校园，某中学组织全校1565名学生参加了“垃圾分类知识竞赛”(满分为100分)，该校数学兴趣小组为了解全校学生竞赛分数情况，采用简单随机抽样的方法(即每名学生的竞赛分数被抽到的可能性相等的抽样方法)抽取部分学生的竞赛分数进行调查分析.(1)以下三种抽样调查方案:方案一：从七年级、八年级、九年级中指定部分学生的竞赛分数作为样本；方案二：从七年级、八年级中随机抽取部分男生的竞赛分数以及在九年级中随机抽取部分女生的竞赛分数作为样本；方案三：从全校1565名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本.其中抽取的样本最具有代表性和广泛性的一种抽样调查方案是__________(填写“方案一”“方案二”或“方案三”);(2)该校数学兴趣小组根据简单随机抽样方法获得的样本，绘制出如下统计表(90分及以上为“优秀”，60分及以上为“及格”，学生竞赛分数记为x分)样本容量平均分及格率优秀率最高分最低分100 83.59 95% 40% 100 52分数段 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100频数 5 7 18 30 40结合上述信息解答下列问题:①样本数据的中位数所在分数段为________；②全校1565名学生，估计竞赛分数达到“优秀”的学生有______人。

某公司要在甲、乙两人中招聘一名职员，对两人的学历、能力、经验这三项进行了测试，各项满分均为10分，成绩高者被录用。左图是甲、乙测试成绩的条形统计图。 (1)分别求出甲、乙三项成绩之和，并指出会录用谁;(2)若将甲、乙的三项测试成绩，按照扇形统计图(右)各项所占之比，分别计算两人各自的综合成绩，并判断是否会改变(1)的录用结果.

2020年2月，贵州省积极响应国家“停课不停学”的号召，推出了“空中黔课”．为了解某中学初三学生每天听空中黔课的时间，随机调查了该校部分初三学生，根据调查结果，绘制出了如下统计图表（不完整），请根据相关信息，解答下列问题：部分初三学生每天听空中黔课时间的人数统计表部分初三学生每天听空中黔课时间的人数统计图（1）本次共调查的学生人数为_____，在表格中，m=______；（2）统计的这组数据中，每天听空中黔课时间的中位数是_____，众数是______；（3）请就疫情期间如何学习的问题写出一条你的看法．

在某次疫情发生后，根据疾控部门发布的统计数据，绘制出如下统计图:图①为A地区累计确诊人数的条形统计图，图②为B地区新增确诊人数的折线统计图. (1)根据图①中的数据，A地区星期三累计确诊人数为__________，新增确诊人数为__________；(2)已知A地区星期一新增确诊人数为14人，在图②中画出表示A地区新增确诊人数的折线统计图.(3)你对这两个地区的疫情做怎样的分析，推断？

为有效推进儿童青少年近视防控工作，教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案(2021-2025年)》，共提出八项主要任务，其中第三项任务为强化户外活动和体育锻炼，我市各校积极落实方案精神，某学校决定开设以下四种球类的户外体育选修课程：篮球、足球、排球、乒乓球，为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程)，并根据调查结果绘制成不完整的统计图表。根据图表信息，解答下列问题:(1)分别求出表中m，n的值;(2)求扇形统计图中“足球”对应的扇形圆心角的度数;(3)该校共有2000名学生，请你估计其中选择“乒乓球”课程的学生人数。

某商场准备进400双滑冰鞋，了解了某段时间内销售的40双滑冰鞋的鞋号，数据如下：鞋号 35 36 37 38 39 40 41 42 43销售量/双 2 4 5 5 12 6 3 2 1根据以上数据，估计该商场进鞋号需求最多的滑冰鞋的数量为______双.

某校举办“歌唱祖国”演唱比赛，十位评委对每位同学的演唱进行现场打分，对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析，下面给出了部分信息。a.甲、乙两位同学得分的折线图： b.丙同学得分：10，10，10，9，9，8，3，9，8，10c.甲、乙、丙三位同学得分的平均数:同学甲乙丙平均数 8.6 8.6 m根据以上信息，回答下列问题：(1)求表中m的值;(2)在参加比赛的同学中，如果某同学得分的10个数据的方差越小，则认为评委对该同学演唱的评价越一致。据此推断：甲、乙两位同学中，评委对______的评价更一致(填“甲”或“乙”);(3)如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分，最后得分越高，则认为该同学表现越优秀，据此推断:在甲、乙、丙三位同学中，表现最优秀的是______(填“甲””“乙”或“丙”).

2013 年起，深圳市实施行人闯红灯违法处罚，处罚方式分为四类:“罚款20元”、“罚款50元”、“罚款 100元”、“穿绿马甲维护交通”，如图是实施首日由某片区的执法结果整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题:(1)实施首日，该片区行人闯红灯违法受处罚一共______；(2)在所有闯红灯违法受处罚的行人中，穿绿马甲维护交通所占的百分比是______%；(3)据了解，“罚款20元”人数是“罚款50元”人数的2倍，请补全条形统计图；(4)根据(3)中的信息，在扇形统计图中，“罚款20元”所在扇形的圆心角等于______度.行人闯红灯违法处罚条形统计图行人闯红灯违法处罚扇形统计图

关于体育选考项目统计图项目频数频率A 80 BB C 0.3C 20 0.1D 40 0.2合计 a 1(1)求出表中a,b,c的值，并将条形统计图补充完整.表中a=______，b=______，c=______. (2)如果有3万人参加体育选考，会有多少人选择篮球?

11月读书节，深圳市为统计某学校初三学生读书状况，如下图： (1)三本以上的x值为______，参加调查的总人数为______，补全统计图；(2)三本以上的圆心角为______；(3)全市有6.7万学生，三本以上有______人.

统计计算

某校九年级进行了3次数学模拟考试，甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分，方差分别是s甲2=3.6，s乙2=4.6，s丙2=6.3，s丁2=7.3，则这4名同学3次数学成绩最稳定的是【】

2020年以来，我国部分地区出现了新冠疫情。一时间，疫情就是命令，防控就是责任，一方有难八方支援.某公司在疫情期间为疫区生产A、B、C、D四种型号的帐篷共20000顶，有关信息见如下统计图：各种型号帐篷数量的百分比统计图每天单独生产各种型号帐篷数量的统计图下列判断正确的是【】

有甲、乙两组数据，如下表所示：甲 11 12 13 14 15乙 12 12 13 14 14甲、乙两组数据的方差分别为S甲2,S乙2则S甲2 ___ S乙2(填“>”，“<”或“=”)。

生物学研究表明，植物光合作用速率越高，单位时间内合成的有机物越多.为了解甲、乙两个品种大豆的光合作用速率，科研人员从甲、乙两个品种的大豆中各选五株，在同等实验条件下，测量它们的光合作用速率(单位：μmol∙m-2∙s-1)，结果统计如下：品种第一株第二株第三株第四株第五株平均数甲 32 30 25 18 20 25乙 28 25 26 24 22 25则两个大豆品种中光合作用速率更稳定的是______(填“甲”或“乙”).

在一次视力检查中，某班7名学生右眼视力的检查结果为：4.2、4.3、4.5、4.6、4.8、4.8、5.0，这组数据的中位数和众数分别是【】

下列数据：75，80，85，85，85，这组数据的众数和极差是【】

某校为了选拔一名百米赛跑运动员参加市中学生运动会，组织了6次预选赛，其中甲，乙两名运动员较为突出，他们在6次预选赛中的成绩（单位：秒）如下表所示：甲 12.0 12.0 12.2 11.8 12.1 11.9乙 12.3 12.1 11.8 12.0 11.7 12.1由于甲，乙两名运动员的成绩的平均数相同，学校决定依据他们成绩的稳定性进行选拔，那么被选中的运动员是______．

为增强学生的环保意识，共建绿色文明校园，某学校组织“废纸宝宝旅行记”活动.经统计，七年级5个班级一周回收废纸情况如下表：则每个班级回收废纸的平均重量为【】班级一班二班三班四班五班废纸重量(kg) 4.5 4.4 5.1 3.3 5.7

某中学九年级举办中华优秀传统文化知识竞赛，用简单随机抽样的方法，从该年级全体600名学生中抽取20名，其竞赛成绩如图:(1)求这20名学生成绩的众数，中位数和平均数;(2)若规定成绩大于或等于90分为优秀等级，试估计该年级获优秀等级的学生人数.

某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下:3，5，3，6，3，4，4，5，2，4，5，6，1，3，5，5，4，4，2，4根据以上数据，得到如下不完整的频数分布表:次数 1 2 3 4 5 6人数 1 2 a 6 b 2(1)表格中的a=______, b=______;(2)在这次调查中，参加志愿者活动的次数的众数为______，中位数为______;(3)若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数.