-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【分析】（1）根据 B点的横坐标为-2 且在反比例函数 y2= 的图象上，可以求得点 B的坐标，然后代入一次函数解析式，即可得到一次函数的解析式，再画出相应的图象即可；
（2）将两个函数解析式联立方程组，即可求得点 C的坐标，然后再观察图象，即可写出当 y1＜y2时对应自变量 x的取值范围；
（3）根据点 B与点 D关于原点成中心对称，可以写出点 D的坐标，然后点 A、D、C的坐标，即可计算出△ACD的面积．
【小问 1详解】 解：∵B点的横坐标为-2 且在反比例函数 y2= 的图象上，
∴点 B的坐标为（-2，-3），
∵点 B（-2，-3）在一次函数 y1=ax-1 的图象上， 解得 a=1，
∴一次函数的解析式为 y=x-1，
∴x=0时，y=-1；x=1时，y=0；
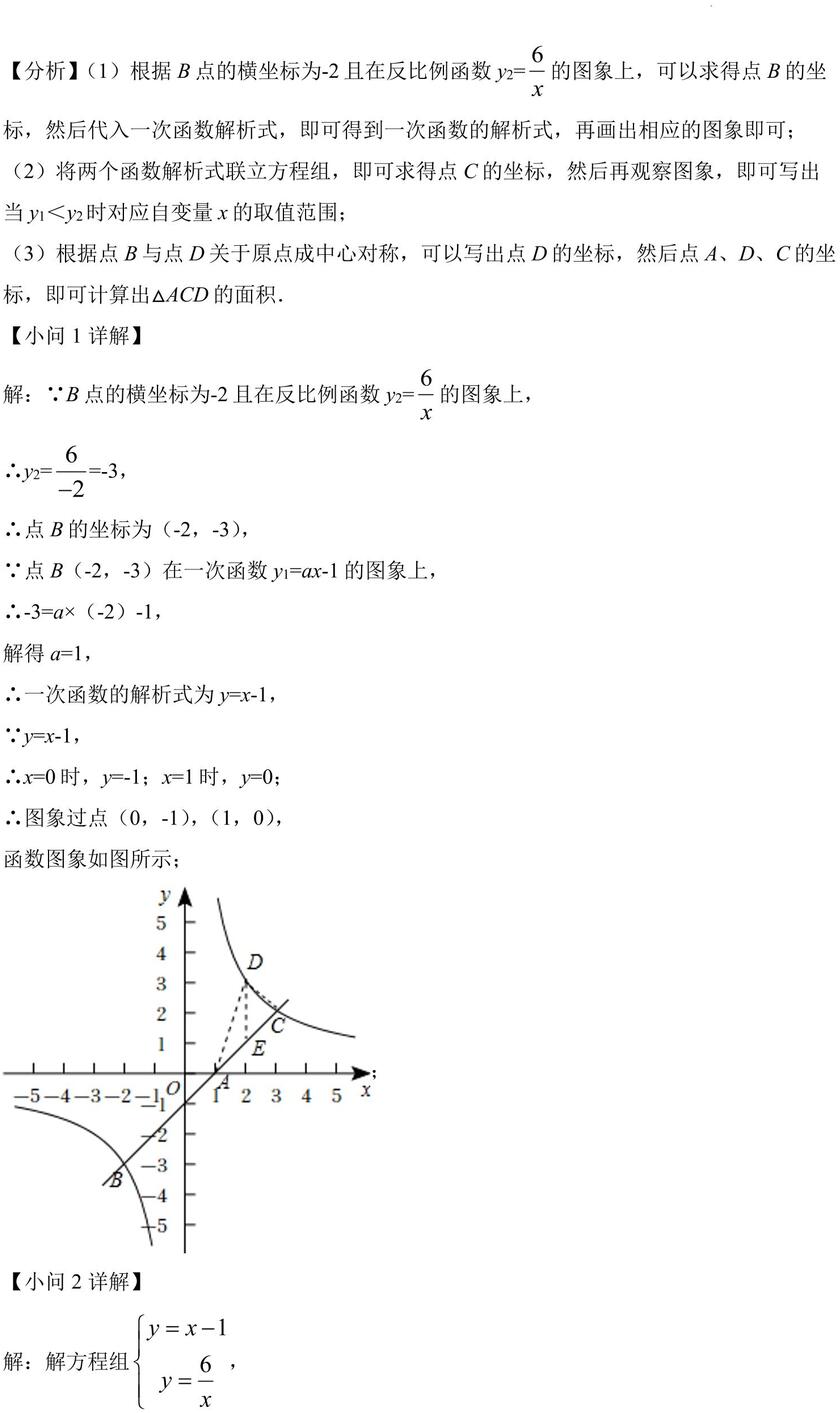
∴图象过点（0，-1），（1，0）， 函数图象如图所示；
【小问 2详解】 解：解方程组 ，