-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【答案】①②③
【分析】根据全等三角形判定即可判断①；过 D 作 DM⊥CA1于 M，利用等腰三角形性质及折叠性质得∠ADE+∠CDM，再等量代换即可判断②；连接 AP、PC、AC，由对称性知，PA1=PA，知 P、A、C共线时取最小值，最小值为 AC 长度，勾股定理求解即可判断
③；过点 A1作 A1H⊥AB 于 H，借助特殊角的三角函数值求出 BE，A1H 的长度，代入三角形面积公式求解即可判断④．
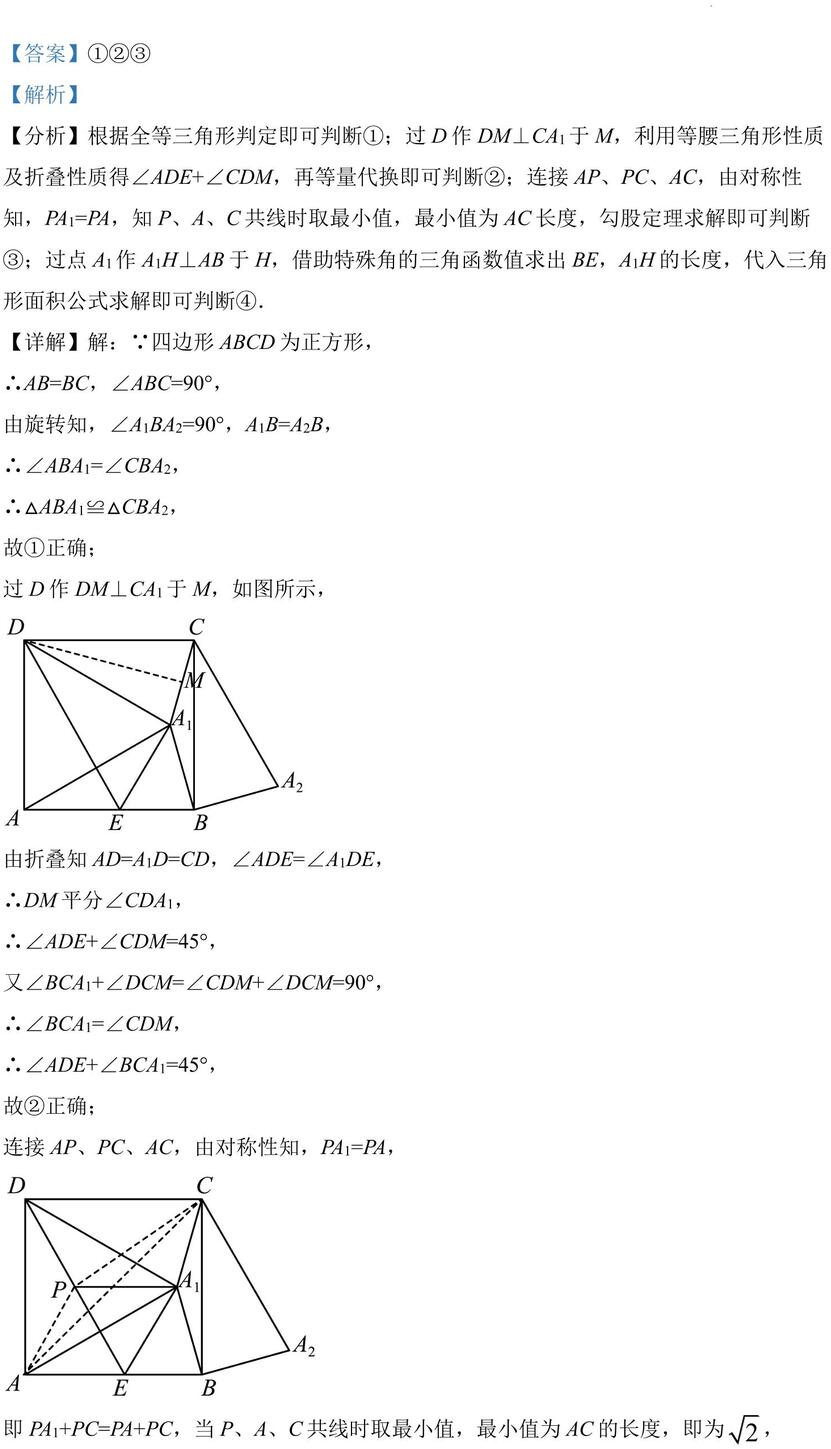
【详解】解：∵四边形 ABCD 为正方形， 由旋转知，∠A1BA2=90°，A1B=A2B， 故①正确； 过 D 作 DM⊥CA1于 M，如图所示， 由折叠知 AD=A1D=CD，∠ADE=∠A1DE，
∴DM 平分∠CDA1， 又∠BCA1+∠DCM=∠CDM+∠DCM=90°， 故②正确； 连接 AP、PC、AC，由对称性知，PA1=PA， 即 PA1+PC=PA+PC，当 P、A、C共线时取最小值，最小值为 AC 的长度，即为 ， 2