-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
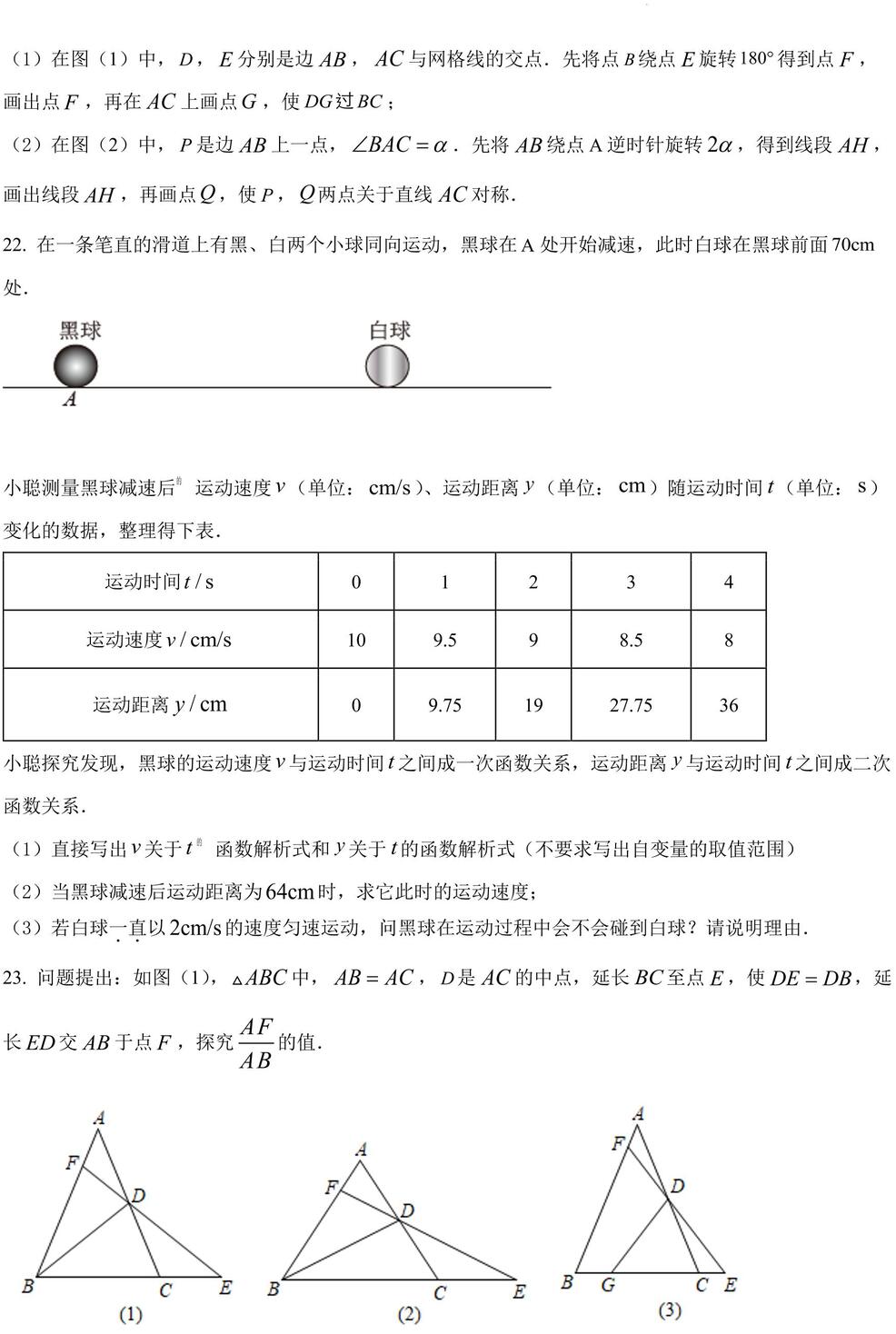
（1）在图（1）中， ， 分别是边 ， 与网格线的交点．先将点 绕点 旋转 得到点 ，画出点 ，再在 上画点 ，使 ；
（2）在图（2）中， 是边 上一点， ．先将 绕点 逆时针旋转 ，得到线段 ，画出线段 ，再画点 ，使 ， 两点关于直线 对称．
22. 在一条笔直的滑道上有黑、白两个小球同向运动，黑球在 处开始减速，此时白球在黑球前面处． 小聪测量黑球减速后 运动速度 （单位： ）、运动距离 （单位： ）随运动时间 （单位： ）变化的数据，整理得下表． 运动时间 0 1 2 3 4 运动速度 10 9.5 9 8.5 8 运动距离 0 9.75 19 27.75 36 小聪探究发现，黑球的运动速度 与运动时间 之间成一次函数关系，运动距离 与运动时间 之间成二次函数关系．
（1）直接写出 关于 函数解析式和 关于 的函数解析式（不要求写出自变量的取值范围）
（2）当黑球减速后运动距离为 时，求它此时的运动速度；
（3）若白球一直．．以 的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由．
23. 问题提出：如图（1）， 中， ， 是 的中点，延长 至点 ，使 ，延长 交 于点 ，探究 的值． 的 v cm/s y cm t s
v t 的 y t