如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿CB方向平移7cm得到线段EF,点E、F分别落在边AB、BC上,则△EBF的周长是______cm.
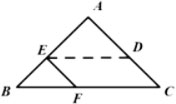
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿CB方向平移7cm得到线段EF,点E、F分别落在边AB、BC上,则△EBF的周长是______cm.

13
【解析】
由平移知:EF∥CD,CF=7,
∴BF=BC-CF=5,∠EFB=∠C=∠B,
∴EF=BE=CD=4,
∴三角形△BEF的周长为:EB+BF+FE=4+4+5=13.
在长方形ABCD中,长为4,宽为2,N为CD的中点,M在AD上,且MBC=BMN,求AM.
如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=【 】
如图,在△ABC中,AB=AC,tan∠B=5/12,D为BC上一点,且满足BD/CD=8/5,过D作DE⊥AD交AC延长线于点E,则CE/AC=______.
如图,等腰直角三角形ABC中,∠A=90°,BC=4.分别以点B、点C为圆心,线段BC长的一半为半径作圆弧,交AB、BC、AC于点D、E、F,则图中阴影部分的面积为________.
如图,在四边形ABCD中,AB=BC=BD.设∠ABC=α,则∠ADC______(用含α的代数式表示).
如图,在ΔABC中,点D,E分别是AB、AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F,求证:ΔABC是等腰三角形.