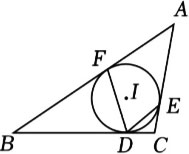
如图,△ABC的内切圆⨀I与BC,CA,AB分别相切于点D,E,F.若⨀I的半径为r,∠A=α,则(BF+CD-BC)和∠FDC的值分别为【 】
A、2r,90°-α
B、0,90°-α
C、2r,90°-α/2
D、0,90°-α/2
如图,△ABC的内切圆⨀I与BC,CA,AB分别相切于点D,E,F.若⨀I的半径为r,∠A=α,则(BF+CD-BC)和∠FDC的值分别为【 】

A、2r,90°-α
B、0,90°-α
C、2r,90°-α/2
D、0,90°-α/2
D∵BD,BF均与⨀I相切,∴BD=BF,同理,CD=CE,∴BF+CD-BC=BD+CD-BC=0.连接IF,IE,则∠EIF=360°-∠A-∠IFE-∠IEF=360°-90°-90°-α=18...
查看完整答案如图,在△ABC中,BC=4,点D、E分别为AB、AC的中点,则DE=【 】
如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.
如图,已知∠AOX=30°,OA=2,AB⊥OA,AB=OA,则B的坐标为________.
在长方形ABCD中,长为4,宽为2,N为CD的中点,M在AD上,且MBC=BMN,求AM.
如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=【 】
如图,在四边形ABCD中,AC与BD相交于点O, ∠ABC=∠DAC=90°,tan∠ACB=1/2,BO/OD=4/3,则S△ABD/S△CBD =________.
如图,四边形ABCD内接于⨀O,AC为⨀O的直径,∠ADB=∠CDB. (1)试判断△ABC的形状,并给出证明;(2)若AB=√2,AD=1,求CD的长度.
如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线垂直,垂足为D.连接并延长BC,交AD的延长线于点E.(1)求证:AE=AB;(2)若AB=10,BC=6,求CD的长.
已知△ABE为直角三角形,∠ABE=90°,BC为圆O的切线,C为切点,CA=CD,则△ABC和△CDE的面积之比为【 】
如图,AB为⊙O的直径,直线 CD与⊙O 相切于点 C,连接AC,若∠ACD=50°,则∠BAC 的度数为【 】
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.