如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA,QD,并过点Q作QO⊥BD,垂足为O,连接OA,OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值。
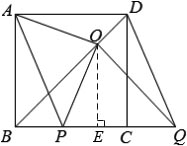

如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA,QD,并过点Q作QO⊥BD,垂足为O,连接OA,OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值。


解答过程见word版
如图,已知△ABC中,D为AB的中点.(1)请用尺规作图法作边AC的中点E,并连接DE (保留作图痕迹,不要求写作法);(2)在(1)条件下,若DE=4,求BC的长.
先化简,再求值:(a+3)/a⋅6/(a²+6a+9)+(2a-6)/(a²-9),其中a=√3-1.
计算:|-3|-(2016+sin30°)0-(-1/2)-1
如图,点P是四边形ABCD外接圆⊙O上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD,连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF=________.
如图,矩形ABCD中,对角线AC=2√3,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B'处,则AB=______.