2022年湖南省怀化市初中学业水平考试(中考)数学试卷

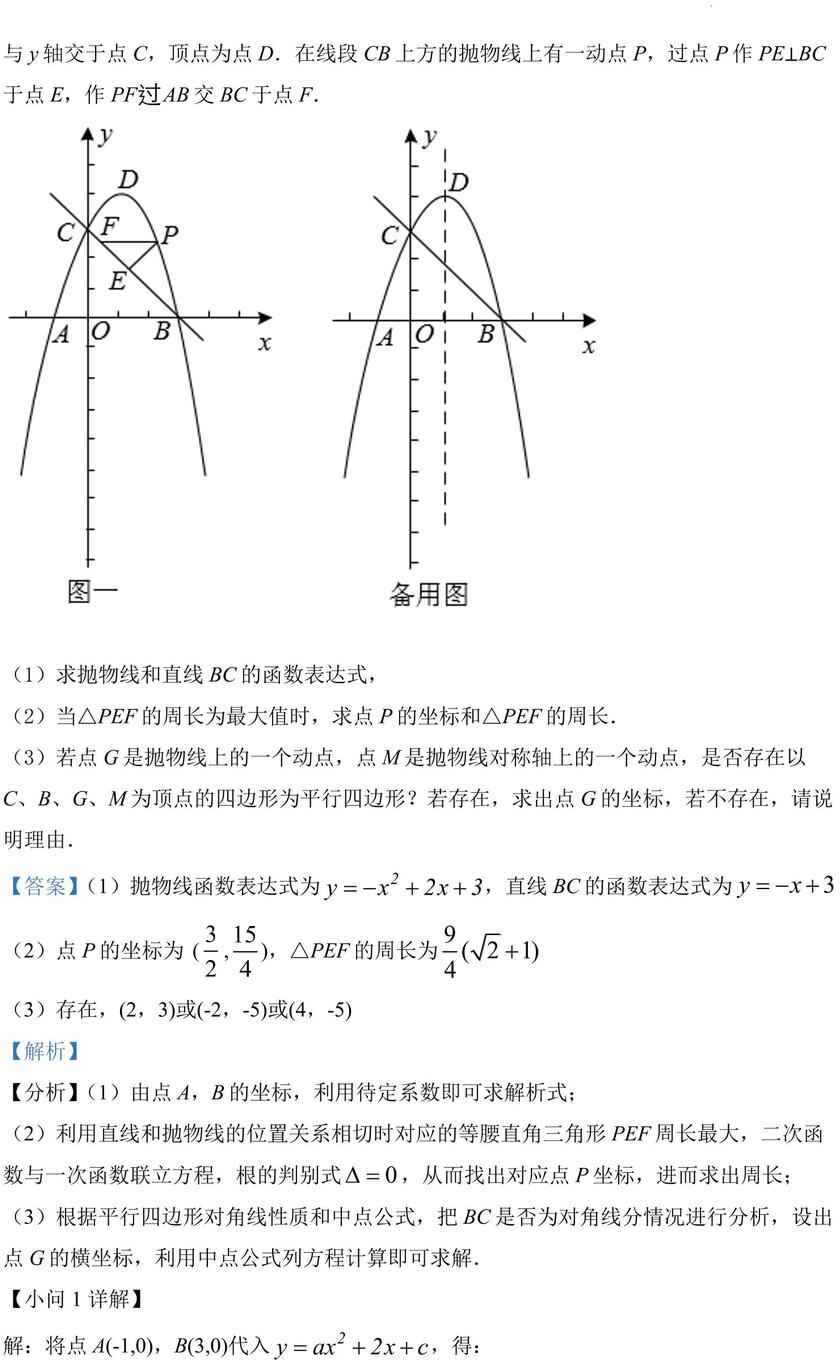
与 y 轴交于点 C，顶点为点 D．在线段 CB 上方的抛物线上有一动点 P，过点 P 作 PE⊥BC于点 E，作 PF AB 交 BC 于点 F．

（1）求抛物线和直线 BC 的函数表达式，

（2）当△PEF 的周长为最大值时，求点 P 的坐标和△PEF 的周长．

（3）若点 G 是抛物线上的一个动点，点 M 是抛物线对称轴上的一个动点，是否存在以

C、B、G、M 为顶点的四边形为平行四边形？若存在，求出点 G 的坐标，若不存在，请说明理由．

【答案】（1）抛物线函数表达式为 ，直线 BC 的函数表达式为

（2）点 P 的坐标为 ( , )，△PEF 的周长为

（3）存在，(2，3)或(-2，-5)或(4，-5)

【分析】（1）由点 A，B 的坐标，利用待定系数即可求解析式；

（2）利用直线和抛物线的位置关系相切时对应的等腰直角三角形 PEF周长最大，二次函数与一次函数联立方程，根的判别式 ，从而找出对应点 P坐标，进而求出周长；

（3）根据平行四边形对角线性质和中点公式，把 BC 是否为对角线分情况进行分析，设出点 G 的横坐标，利用中点公式列方程计算即可求解．

【小问 1详解】 解：将点 A(-1,0)，B(3,0)代入 ，得：