-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【分析】（1）根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心，故只要作出两个角的角平分线即可；
（2）利用割补法，连接 OA，OB，OC，作 OD⊥AB，OE⊥BC，OF⊥AC，这样将△ABC分成三个小三角形，这三个小三角形分别以△ABC 的三边为底，高为内切圆的半径，利用提取公因式可将周长代入，进而求出三角形的面积．
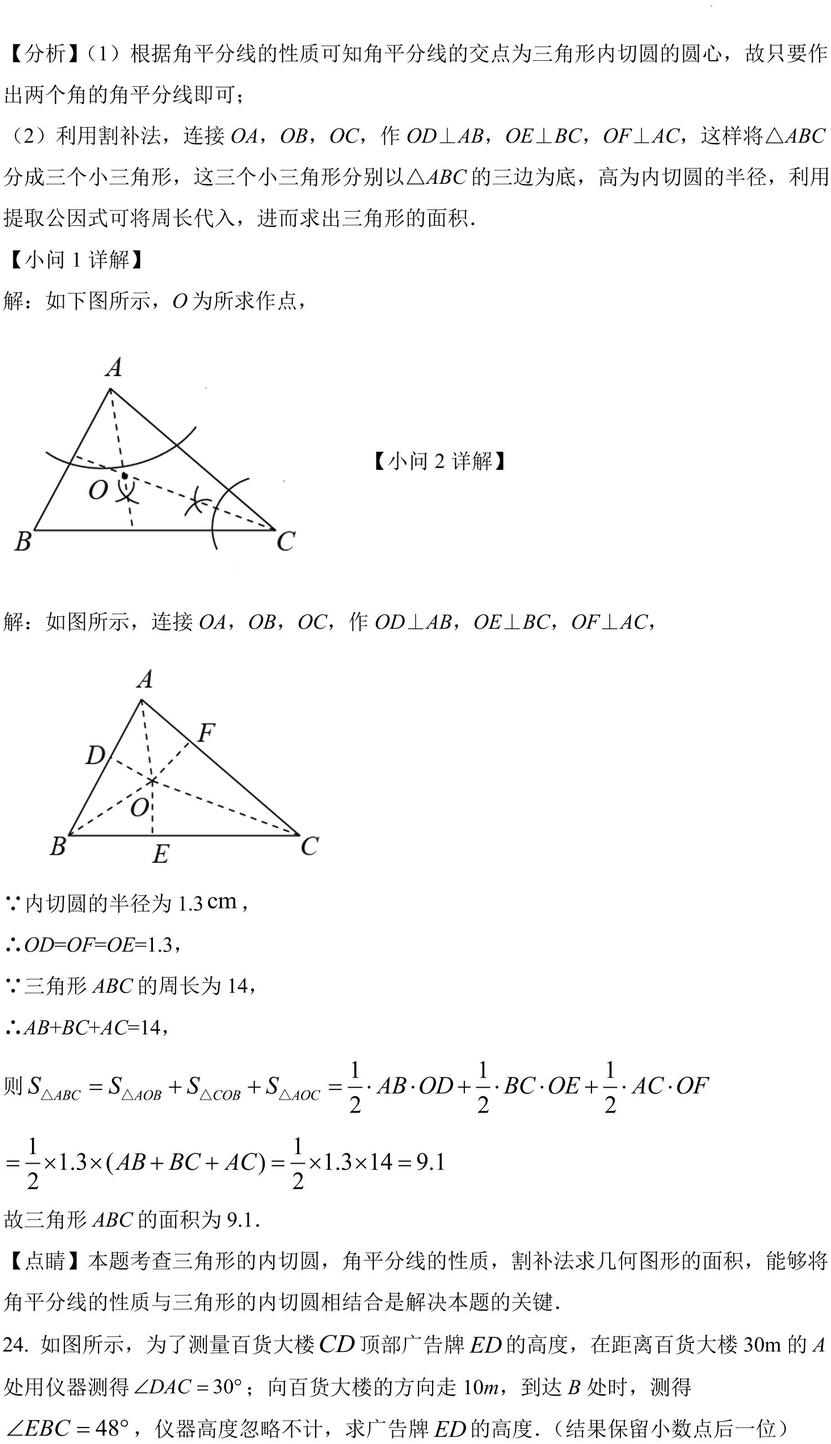
【小问 1详解】 解：如下图所示，O 为所求作点，
【小问 2详解】 解：如图所示，连接 OA，OB，OC，作 OD⊥AB，OE⊥BC，OF⊥AC，
∵内切圆的半径为 1.3 ，
∵三角形 ABC 的周长为 14， 则 故三角形 ABC 的面积为 9.1．
【点睛】本题考查三角形的内切圆，角平分线的性质，割补法求几何图形的面积，能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键．
24. 如图所示，为了测量百货大楼 顶部广告牌 的高度，在距离百货大楼 30m 的 A处用仪器测得 ；向百货大楼的方向走 10m，到达 B处时，测得
，仪器高度忽略不计，求广告牌 的高度．（结果保留小数点后一位）