初中数学-中考试题(广东省广州市 2020年全等)

问答题（2020年广东省广州市）

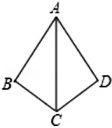
如图，AB=AD,∠BAC=∠DAC=25°,∠D=80°，求∠BCA的度数.

答案解析

解答过程见word版

讨论

全等

如图，已知∠AOC=∠BOC，点P在OC上，PD⊥OA,PE⊥OB，垂足分别为D,E.求证：△OPD≌△OPE.

如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S△ABF=S△ADF；②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是【】

如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．(1)求证：△ADE≌△CED；(2)求证：△DEF是等腰三角形．

如图，B是AD的中点，BC//DE,BC=DE.求证：∠C=E.

如图，点D,E在△ABC的边BC上，∠B=∠C,BD=CE,求证：△ABD≌△ACE.

在△ABC中，∠ACB=90°，D为△ABC内一点，连接BD，DC延长DC到点E，使得CE=DC. (1)如图(左)，延长BC到点F，使得CF=BC，连接AF、EF，若AF⊥EF，求证：BD⊥AF.(2)连接AE，交BD的延长线干点H，连接CH，依题意补全图(右)，若AB²=AE²+BD²，用等式表示线段CD与CH的数量关系，并证明.

如图，四边形ABCD中，AD//BC,∠ABC=90°,∠C=30°,AD=3,AB=2√3,DH⊥BC于点H,将△PQM与该四边形按如图方式放在同一平面内，使点P与A重合，点B在PM上，其中∠Q=90°,∠QPM=30°,PM=4√3. (1)求证：△PQM≅△CHD;(2) △PQM从图1的位置出发，先沿着BC方向向右平移(图2)，当点P到达点D后立刻绕点D逆时针旋转(图3)，当边PM旋转50°时停止.①边PQ从平移开始，到绕点D旋转结束，求边PQ扫过的面积;②如图2点K在BH上，且BK=9-4√3.若△PQM右移的速度为每秒1个单位长，绕点D旅转的速度为每秒5°，求点K在△PQM区域(含边界)内的时长;③如图3在△PQM旋转过程中，设PQ,PM分别交BC于点E,F，若BE=d，直接写出CF的长(用含d的式子表示).

如图，点E、F在线段BC上，AB//CD，∠A=∠D,BE=CF，证明：AE=DF.

如图，△ABC和△DEF中，AB=DE，∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF【】

如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN=45°.把ΔADN绕点A顺时针旋转90°得到ΔABE. （1）求证：ΔAEM≌ΔANM.（2）若BM=3，DN=2，求正方形ABCD的边长.

三角形

下列图形中具有稳定性的是【】

如图，在△ABC中，BC=4，点D、E分别为AB、AC的中点，则DE=【】

如图，已知∠AOX=30°,OA=2,AB⊥OA,AB=OA，则B的坐标为________.

在长方形ABCD中，长为4，宽为2，N为CD的中点，M在AD上，且MBC=BMN,求AM.

如图，在△ABC中，AB=AC,tanB=3/4，点D为BC上一动点，连接AD，将△ABD沿AD翻折得到△ADE,DE交AC于点G,GE<DG，且AG:CG=3:1，则S△AGE/S△ADG =________.

如图，已知AB=AC,BC=6，尺规作图痕迹可求出BD=【】

如图，在四边形ABCD中，AC与BD相交于点O, ∠ABC=∠DAC=90°,tan∠ACB=1/2,BO/OD=4/3，则S△ABD/S△CBD =________.

已知△ABC是直角三角形，∠B=90°,AB=3,BC=5,AE=2√5，连接CE，以CE为底作直角三角形CDE,CD=DE. F是AE边上的一点，连接BD,BF,∠FBD=45°，则AF长为________.

如图，已知△ABC∽△EDC，AC:EC=2:3，若AB的长度为6，则DE的长度为【】

设D为△ABC的外接圆弧 BC(不含点A)上一点，且满足 AB:AC =DB:DC.设点 B'为B关于 AC 的对称点，点C'为C关于AB 的对称点，点D'为D关于BC的对称点.求证：△BCD与△B'C'D'相似.

几何图形

下列出版社的商标图案中，是轴对称图形的为【】

如图，街道AB与CD平行，拐角∠ABC=137°，则拐角∠BCD = 【】

如图，AB是⊙O的直径，∠BAC=50°,则∠D=【】

边长分别为10，6，4的三个正方形拼接在一起，它们的底边在同一直线上(如图)，则图中阴影部分的面积为________.

如图，在▱ABCD 中，∠DAB=30°.(1)实践与操作：用尺规作图法过点D作AB边上的高DE；(保留作图痕迹，不要求写作法)(2)应用与计算：在(1)的条件下，AD=4，AB=6，求BE的长.

综合与实践主题：制作无盖正方体形纸盒.素材：一张正方形纸板步骤1：如图1，将正方形纸板的边长三等分，画出九个相同的小正方形，并剪去四个角上的小正方形；步骤2：如图2，把剪好的纸板折成无盖正方体形纸盒. 猜想与证明:(1)直接写出纸板上∠ABC 与纸盒上∠A1B1C1的大小关系:(2)证明 (1)中你发现的结论.

综合探究如图1，在矩形ABCD中（AB>AD），对角线AC,BD相交于点O，点A关于BD的对称点为A'.连接AA'交BD于点E，连接CA'. (1)求证：AA'⊥CA'；(2)以点O为圆心，OE为半径作圆.①如图2，⨀O与CD相切，求证：AA'=√3 CA'；②如图3，⨀O与CA'相切，AD=1，求⨀O的面积.

如图，直线a，b被直线c所截，a//b，∠1=40°，则∠2等于【】

如图，在▱ABCD中，一定正确的是【】

菱形的边长为5，则它的周长为______.