如图,点E,F分别在正方形ABCD的边BC、CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.
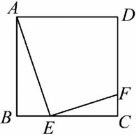
如图,点E,F分别在正方形ABCD的边BC、CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.

∵BE=3,EC=6,
∴BC=9,
∵四边形ABCD是正方形,
∴AB=BC=9,∠B=∠C=90°,
又∵AB/CE=9/6=3/2=BE/CF,
∴△ABE∼△ECF.
如图,已知△ABC∽△EDC,AC:EC=2:3,若AB的长度为6,则DE的长度为【 】
若两个相似三角形的周长比为2:3,则它们的面积比是________.
如图,BC//DE,且BC<DE,AD=BC=4,AB+DE=10,则AE/AC的值为__________.
在Rt△ABC中,∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F,且AF=4,EF=√2,则AC=________.
如图,每个小正方形边长均为1,则图中的三角形(阴影部分)与下图中△ABC相似的是【 】
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为【 】
泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】
如图,在ΔABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为_________.
边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为________.
如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF,若AB=2,则OF的长度为【 】
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求BG的长.
如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为【 】
如图,在正方形ABCD中,点P从点A出发,沿正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x形成的函数关系图像大致是【 】
完全相同的4个正方形面积之和是 100,则正方形的边长是【 】
如图所示,四边形 ABCD,DEFG,GHIJ 均为正方形,且SABCD=10,SGHI=1,则正方形 DEFG 的边长可以是________(写出一个答案即可).
如图,正方形ABCD的边长为4,点E在边BC上,且BE=1,F为对角线BD上一动点,连接CF,则CF+EF的最小值为______.
如图,在△ABC中,BC=4,点D、E分别为AB、AC的中点,则DE=【 】
如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.
如图,已知∠AOX=30°,OA=2,AB⊥OA,AB=OA,则B的坐标为________.
在长方形ABCD中,长为4,宽为2,N为CD的中点,M在AD上,且MBC=BMN,求AM.
如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=【 】
如图,在四边形ABCD中,AC与BD相交于点O, ∠ABC=∠DAC=90°,tan∠ACB=1/2,BO/OD=4/3,则S△ABD/S△CBD =________.