• 关注优题吧，注册平台账号.

题吧，智能辅助学习中心
  2. 初中数学
  3. 式
  4. 二次根式
  2. 知识库
  3. 试卷库

填空题（2021年云南省）

已知a,b都是实数，若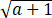+(b-2)2=0，则a-b=__________.

答案解析

-3

讨论

初中数学

2020年以来，我国部分地区出现了新冠疫情。一时间，疫情就是命令，防控就是责任，一方有难八方支援.某公司在疫情期间为疫区生产A、B、C、D四种型号的帐篷共20000顶，有关信息见如下统计图：各种型号帐篷数量的百分比统计图每天单独生产各种型号帐篷数量的统计图 下列判断正确的是【 】

如图，等边△ABC的三个顶点都在⨀O上，AD是⨀O的直径.若OA=3，则劣弧BD的长是【 】

按一定规律排列的单项式：a2,4a3,9a4,16a5,25a6,…，第n个单项式是【 】

若一元二次方程ax2+2x+1=0有两个不相等的实数根，则实数a的取值范围是【 】

在△ABC中，∠ABC=90°，若AC=100,sinA=3/5，则AB的长是【 】

一个10边形的内角和等于【 】

如图，直线c与直线a、b都相交，若a//b，∠1=55°，则∠2=【 】

某地区2021年元旦的最高气温为9°，最低气温为-2°，那么该地区这天的最低气温比最高气温低【 】

由沈康身教授所著，数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事：如图，三姐妹为了平分一块边长为1的祖传正方形地毯，先将地毯分割成七块，再拼成三个小正方形(阴影部分).则图中AB的长应是________.

已知在平面直角坐标系xOy中，点A的坐标为(3,4)，M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点.小明经探究发现：当b/a的值确定时，抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.若抛物线y=ax2+bx+2(a≠0)的对称轴上存在3个不同的点M，使△AOM为直角三角形，则b/a的值是______.

二次根式

若式子在实数范围内有意义，则x的取值范围是________.

计算-的结果是________.

若式子在实数范围内有意义，则x的取值范围是【 】

计算：√18×√(1/2)的结果为______.

代数式在实数范围内有意义时，x应满足的条件是__________.

计算(√27-√12)×√(1/3)的结果是【 】

若在实数范围内有意义，则实数x的取值范围是__________.

若在实数范围内有意义，则实数x的取值范围是________.

为庆祝中国共产党成立100周年，某市组织该市七、八两个年级学生参加演讲比赛，演讲比赛的主题为“追忆百年历程，凝聚青春力量”，该市一中学经过初选，在七年级选出3名同学，其中2名女生，分别记为x1、x2，1名男生，记为y1;在八年级选出3名同学，其中1名女生，记为x3,2名男生，分别记为y2,y3，现分别从两个年级初选出的同学中，每个年级随机选出一名同学组成代表队参加比赛.(1)用列表法或树状图法(树状图也称树形图)中的一种方法，求所有可能出现的代表队总数;(2)求选出的代表队中的两名同学恰好是一名男生和一名女生的概率P.

已知抛物线y=-2x2+bx+c经过点(0,-2)，当x<-4时，y随x的增大而增大，当x>-4时，y随x的增大而减小.设r是抛物线y=-2x2+bx+c与x轴的交点（也称公共点）的横坐标，m=(r9+r7-2r5+r3+r-1)/(r9+60r5-1).(1)求b,c的值；(2)求证：r4-2r2+1=60r2；(3)以下结论：m<1,m=1,m>1，你认为哪个正确？请证明你的结论.

式

计算： + (-1/2)-1 - 2cos60° + (2-π)0 .

先化简，再求值(x2 + 4x + 4)/(x + 2) ÷ (x2 + 2x)，其中x=.

先化简分式(a2-9)/(a2+6a+9)÷(a-3)/(a2+3a)-(a-a2)/(a-1)，然后在0，1，2，3中选一个你认为合适的a值，代入求值.

下列运算正确的是【 】

计算：+|2|-32.

先化简，再求值：(1+1/(x-1))∙(x2-1)/x，其中x=-1.

计算(a2)3∙a-3的结果是【 】

计算(a/(b2+ab)-2/(a+b)+b/(a2+ab))÷(a-b)/ab.

计算(√19+1)(√19-1)的结果等于________.

先化简，再求值：(3x/(x-2)-x/(x+2))÷x/(x²-4)，在-2,0,1,2四个数中选一个合适的代入求值.