-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【点睛】本题考查了解分式方程，掌握分式方程的一般解法是解题的关键．
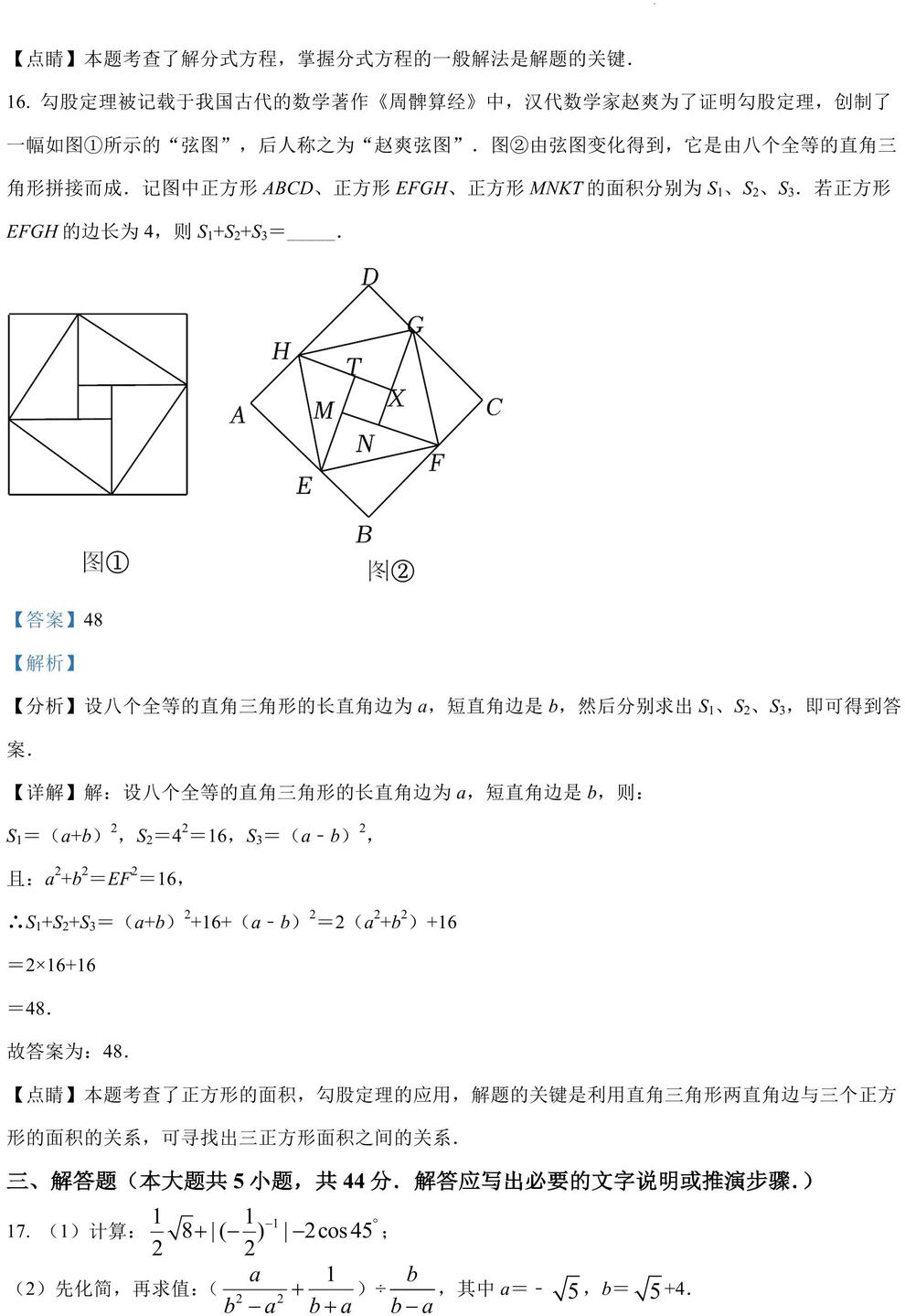
16. 勾股定理被记载于我国古代的数学著作《周髀算经》中，汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”．图②由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形 ABCD、正方形 EFGH、正方形 MNKT 的面积分别为 S1、S2、S3．若正方形
EFGH 的边长为 4，则 S1+S2+S3＝_____．
【答案】48
【分析】设八个全等的直角三角形的长直角边为 a，短直角边是 b，然后分别求出 S1、S2、S3，即可得到答案．
【详解】解：设八个全等的直角三角形的长直角边为 a，短直角边是 b，则： 且：a2+b2＝EF2＝16， 故答案为：48．
【点睛】本题考查了正方形的面积，勾股定理的应用，解题的关键是利用直角三角形两直角边与三个正方形的面积的关系，可寻找出三正方形面积之间的关系．
三、解答题（本大题共 5小题，共 44分．解答应写出必要的文字说明或推演步骤．）
17. （1）计算： 1
（2）先化简，再求值：（ 2 2
，其中 a＝﹣ 5，b＝ 5 +4．