-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
解：若△AOB和△DPC 全等，且∠AOB=∠DPC=90°， 分两种情况：
①△AOB≌△DPC，则 AO=PD=1，OB=PC=2，
∴点 P 的坐标为(1，0)；
②△AOB≌△CPD，则 OB=PD=2，
∴正方形 OPDE 的边长为 2，
∴点 P 的坐标为(2，0)； 综上，点 P 的坐标为(1，0)或(2，0)；
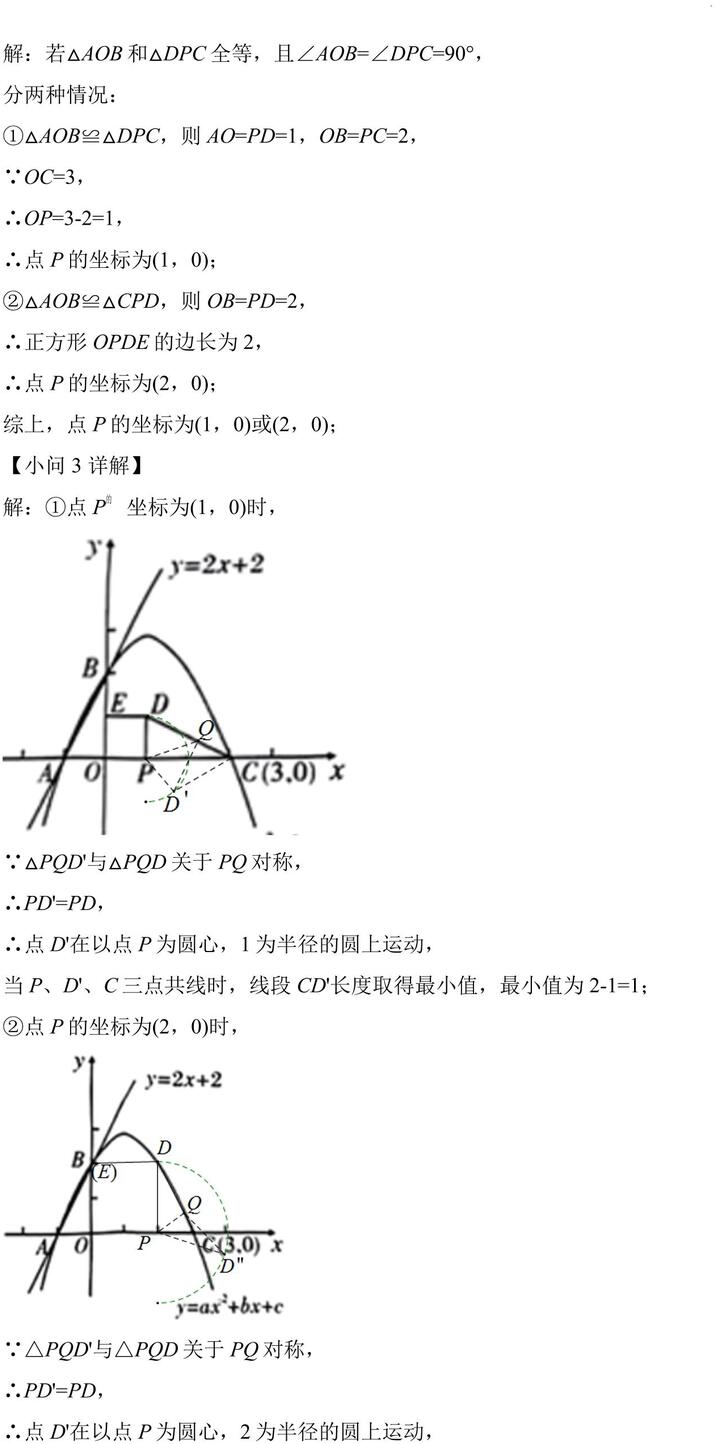
【小问 3详解】 解：①点 P 坐标为(1，0)时，
∵△PQD与△PQD 关于 PQ 对称，
∴点 D在以点 P 为圆心，1 为半径的圆上运动，当 P、D、C 三点共线时，线段 CD长度取得最小值，最小值为 2-1=1；
②点 P 的坐标为(2，0)时，
∵△PQD与△PQD 关于 PQ 对称，
∴点 D在以点 P 为圆心，2 为半径的圆上运动，