把一盒长方体包装的牛奶(如图),倒入底面积是20cm2、高是8cm的圆柱形杯子里,至少能倒满几杯?
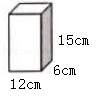
把一盒长方体包装的牛奶(如图),倒入底面积是20cm2、高是8cm的圆柱形杯子里,至少能倒满几杯?

牛奶的体积为12×6×15=1080(cm3)
圆柱形杯子的容积为:20×8=160(cm3)
1080÷160=6.75,所以至少能倒满6杯。
下图是一个长方体的表面展开图(单位: cm )。这个长方体的体积是______cm3。
一个长方体,如下图所示,这个长方体的棱长之和是______分米。
用一根长48dm的铁丝作一个长方体框架,使它的高为6dm,长、宽的比为1:1。再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸?
棱长为2分米的正方体,它的表面积是__________平方分米,3个这样的正方体拼成一个长方体,拼成的长方体的表面积是__________平方 分米。
一个长方体木块的长、宽、高分别是5cm、4cm、3cm。如果把它锯 成一个最大的正方体,得到的正方体的体积比原来长方体的体积减小__________。(结果用百分数表示)
从由8个棱长是1厘米的小正方体拼成的大正方体中,拿走一个 小正方体,这时它的表面积是【 】平方厘米。
把一个长为8厘米,宽为6厘米,高为4厘米的长方体切成两个长方体,下图中【 】的切法增加的表面积多。① ② ③
用棱长是1cm的正方体,拼成一个长4cm、宽3cm、高2cm的长方体,需要__________块小正方体,拼成的长方体的表面积是__________cm2。
下图扇形的半径是 r 。请你想象,用这个扇形围成一个高为 h 的圆锥(接缝处不计) , 圆锥的高 h 与扇形半径 r 之间的关系是【 】。
一个圆柱形橡皮泥,底面半径是2厘米,高是5厘米。(1)这个橡皮泥的表面积是多少平方厘米?(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
下列选项中各图形以虚线为轴旋转一周形成几何体,【 】图形成的体积与下图形成的体积相等。
一个长方体模型,从前面看是,从上面看是,这个长方体的体积是__________cm3。
一个棱长为a米的正方体,任意截成两个长方体,则两个长方体的表面积之和是【 】a2平方米。
用一根长24分米的铁丝做一个长方体框架,使它的长、宽、高的 比是5:4:3。这个长方体的体积是【 】立方分米。