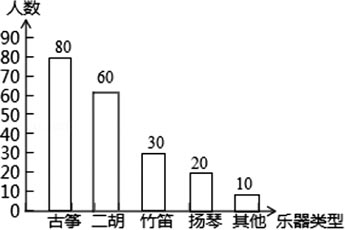
某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.

(1)这次共抽取______名学生进行调查,扇形统计图中的x=______;
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是______度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有______名.
某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.

(1)这次共抽取______名学生进行调查,扇形统计图中的x=______;
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是______度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有______名.
(1)200 15%
(2)补全统计图如下:
(3)36°
(4)900
(解答过程见word版)