关注优题吧，注册平台账号.
如图1，抛物线y=ax2+2x+c经过点A(-1,0),C(0,3)，并交x轴于另一点B，点P(x,y)在第一象限的抛物线上，AP交直线BC于点D.
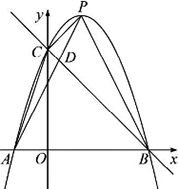
(1)求该抛物线的函数表达式;
(2)当点P的坐标为(1,4)时，求四边形BOCP的面积;
(3)点Q在抛物线上，当PD/AD的值最大且△APQ是直角三角形时，求点Q的横坐标;
(4)如图2，作CG⊥CP,CG交x轴于点G(n,0)，点H在射线CP上，且CH=CG,过GH的中点K作KI//y轴，交抛物线于点I，连接IH，以IH为边作出如图所示正方形HIMN，当顶点M恰好落在y轴上时，请直接写出点G的坐标。
(1)∵抛物线y=ax2+2x+c经过点A(-1,0),C(0,3)，∴，解得∴该抛物线的函数表达式为y=-x2+2x+3.(2)如图，连接OP，令y=-x2+2x+3=0，解得x1=-1,x2=3，∴B(3,0).∵C(0,3),P(1,4),∴OC=3,OB=3,xP=1,yP=4.∴S△POC=1/2 OC⋅xP=3/2,S△BOP=1/2 OB⋅yP=6,∴S四边形BOCP=S△POC+S△BOP=15/2.(3)如图，作PF//x轴，交直线BC于点F，则△PFD∼△ABD,∴PD/AD=PF/AB.∵AB=4是定值，∴当PF最大时，PD/AD=PF/AB最大.设yBC=kx+b，∵C(0,3),B(3,0),∴yBC=-x+3.设P(m,-m2+2m+3)，则F(m2-2m,-m2+2m+3).∴PF=m-(m2-2m)=-m2+3m=-(m-3/2)2+9/4.∴当m=3/2时，PF取得最大值9/4，此时P(3/2,15/4).设点Q(t,-t2+2t+3)，若△APQ是直角三角形，则点Q不能与点P,A重合，∴t≠3/2,t≠1，下面分三类情况讨论：①...
查看完整答案