初中数学-中考试题(广东省深圳市 2010年数据处理)

问答题（2010年广东省深圳市）

低碳发展是今年深圳市政府工作报告提出的发展理念,近期,某区与某技术支持单位合作,组织策划了该区“低碳先锋行动”,开展低碳测量和排行活动,根据调查数据制作了频数分布直方图和扇形统计图,图1中从左到右各长方形的高度之比为2:8:9:7:3:1.

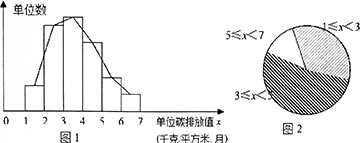
(1)已知碳排放值5≤x<7(千克平方米·月)的单位有16个,则此次行动共调查了______个单位；

(2)在图2中,碳排放值5≤x<7(千克/平方米月)部分的圆心角为______度；

(3)小明把图1中碳排放值1≤x<2的都看成1.5,碳排放值2≤x<3的都看成2.5,以此类推,若每个被检查单位的建筑面积均为10000平方米,则按小明的办法,可估算碳排放值x≥4(千克/平方米月)的被检单位一个月的碳排放总值约为______吨.

答案解析

(1) 16÷(3+1)/(2+8+9+7+3+1)=120(个)(2) 16÷120×360°=48°(3)碳排放值x≥4千克/平方米•月的被检单位是第4，5，6组，7/(2+8+9+7+3+1)×120=28,...

查看完整答案

讨论

初中数学

先化简分式(a2-9)/(a2+6a+9)÷(a-3)/(a2+3a)-(a-a2)/(a-1)，然后在0，1，2，3中选一个你认为合适的a值，代入求值.

(1/3)-2-2sin45°+(π-3.14)0+1/2 +(-1)3.

如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行______分钟可使渔船到达离灯塔距离最近的位置.

如图所示,是一个由若干个相同的小正方体组成的几何体的主视图(左)和俯视图(右),则能组成这个几何体的小正方体的个数最少是______个。

如图所示,在▱ABCD中,AB=5,AD=8,DE平分∠ADC,则BE=________.

分解因式：4x2-4=____________.

如图所示,点P(3a,a)是反比例函数y=k/x(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【】

某单位向一所希望小学赠送1080件文具,现用A,B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.设B型包装箱每个可以装x件文具,根据题意列方程式为【】

有四张质地相同的卡片,它们的背面相同,其中两张的正面印有“粽子”的图标,另外两张的正面印有“龙舟”的图案,现将它们背面朝上,洗均匀后排列在桌面,任意翻开两张,那么两张图案一样的概率是【】

如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是【】

统计初步

首届全民阅读大会于2022年4月23日在北京开幕，大会主题是“阅读新时代·奋进新征程”某校“综合与实践”小组为了解全校3600名学生的读书情况，随机抽取部分学生进行问卷调查，形成了如下调查报告(不完整)：××中学学生读书情况调查报告请根据以上调查报告，解答下列问题：(1)求参与本次抽样调查的学生人数及这些学生中选择“从图书馆借阅”的人数；(2)估计该校3600名学生中，平均每周阅读课外书时间在“8小时及以上”的人数；(3)该小组要根据以上调查报告在全班进行交流，假如你是小组成员，请结合以上两项调查数据分别写出一条你获取的信息.

2013 年起，深圳市实施行人闯红灯违法处罚，处罚方式分为四类:“罚款20元”、“罚款50元”、“罚款 100元”、“穿绿马甲维护交通”，如图是实施首日由某片区的执法结果整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题:(1)实施首日，该片区行人闯红灯违法受处罚一共______；(2)在所有闯红灯违法受处罚的行人中，穿绿马甲维护交通所占的百分比是______%；(3)据了解，“罚款20元”人数是“罚款50元”人数的2倍，请补全条形统计图；(4)根据(3)中的信息，在扇形统计图中，“罚款20元”所在扇形的圆心角等于______度.行人闯红灯违法处罚条形统计图行人闯红灯违法处罚扇形统计图

关于体育选考项目统计图项目频数频率A 80 BB C 0.3C 20 0.1D 40 0.2合计 a 1(1)求出表中a,b,c的值，并将条形统计图补充完整.表中a=______，b=______，c=______. (2)如果有3万人参加体育选考，会有多少人选择篮球?

11月读书节，深圳市为统计某学校初三学生读书状况，如下图： (1)三本以上的x值为______，参加调查的总人数为______，补全统计图；(2)三本以上的圆心角为______；(3)全市有6.7万学生，三本以上有______人.

深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况，某校数学兴趣小组随机采访部分深圳市民，对采访情况制作了统计图表的一部分如下:关注情况频数频率A.高度关注 M 0.1B.一般关注 100 0.5C.不关注 30 ND.不知道 50 0.25东进战略关注情况条形统计图(1)根据上述统计图可得此次采访的人数为________人，M = ________，N = ________；(2)根据以上信息补全条形统计图；(3)根据上述采访结果，请估计在 15000 名深圳市民中，高度关注东进战略的深圳市民约有________人.

深圳市某学校抽样调查，A 类学生骑共享单车，B 类学生坐公交车、私家车等，C类学生步行，D类学生(其它)，根据调查结果绘制了不完整的统计图.类型频数频率A 30 xB 18 0.15C m 0.40D n y(1) 学生共______人，x=______，y=______；(2)补全条形统计图；(3)若该校共有 2000 人，骑共享单车的有______人.

某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形图：频数频率体育 40 0.4科技 25 a艺术 b 0.15其它 20 0.2请根据上图完成下面题目：(1)总人数为______人，a=______，b=______.(2)请你补充全条形统计图.(3)若全校有600人，请你估算一下全校喜欢艺术的学生人数有多少？

为了解天水市民对全市创建全国文明城市工作的满意程度，某中学数学兴趣小组在某个小区内进行了调查统计.将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图.请结合图中的信息，解决下列问题：（1）此次调查中接受调查的人数为__________人；（2）请你补全条形统计图；（3）扇形统计图中“满意”部分的圆心角为__________度；（4）该兴趣小组准备从调查结果为“不满意”的4位市民中随机选择2位进行回访，已知这4位市民中有2位男性，2位女性.请用画树状图的方法求出选择回访的市民为“一男一女”的概率.

某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生选且只能选其中一个等级.随机抽取了120名学生的有效问卷，数据整理如下：等级非常了解比较了解基本了解不太了解人数（人）247218x（1）求x的值；（2）若该校有学生1800人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？

在某次疫情发生后，根据疾控部门发布的统计数据，绘制出如下统计图:图①为A地区累计确诊人数的条形统计图，图②为B地区新增确诊人数的折线统计图. (1)根据图①中的数据，A地区星期三累计确诊人数为__________，新增确诊人数为__________；(2)已知A地区星期一新增确诊人数为14人，在图②中画出表示A地区新增确诊人数的折线统计图.(3)你对这两个地区的疫情做怎样的分析，推断？

数据处理

为培养学生的阅读习惯，某中学利用学生课外时间开展了以“走近名著”为主题的读书活动.为了有效了解学生课外阅读情况，现随机调查了部分学生每周课外阅读的时间，设被调查的每名学生每周课外阅读的总时间为x小时，将它分为4个等级：A（0≤x<2），B（2≤x<4），C（4≤x<6），D（x≥6），并根据调查结果绘制了如两幅不完整的统计图：请你根据统计图的信息，解决下列问题：（1）本次共调查了_________名学生；（2）在扇形统计图中，等级D所对应的扇形的圆心角为_________°；（3）请补全条形统计图；（4）在等级D中有甲、乙、丙、丁4人表现最为优秀，现从4人中任选2人作为学校本次读书活动的宣传员，用列表或画树状图的方法求恰好选中甲和乙的概率.

随机调查某城市30天空气质量指数(AQI)，绘制成如下扇形统计图。空气质量等级空气质量指数(AQI) 频数优 AQI≤50 m良 50<AQI≤100 15中 100<AQI≤150 9差 AQI>150 n(1)m=_____,n=_____;(2)求良的占比;(3)求差的圆心角;(4)折线图是一个月内的空气污染指数统计，然后根据这个一个月内的统计进行估测一年的空气污染指数为中的天数，从折线图可以得到空气污染指数为中的有9天.根据折线统计图，一个月(30天)中有_____天AQI为中，估测该城市一年(以365天计)中大约有______天AQI为中.

为有效推进儿童青少年近视防控工作，教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案(2021-2025年)》，共提出八项主要任务，其中第三项任务为强化户外活动和体育锻炼，我市各校积极落实方案精神，某学校决定开设以下四种球类的户外体育选修课程：篮球、足球、排球、乒乓球，为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程)，并根据调查结果绘制成不完整的统计图表。根据图表信息，解答下列问题:(1)分别求出表中m，n的值;(2)求扇形统计图中“足球”对应的扇形圆心角的度数;(3)该校共有2000名学生，请你估计其中选择“乒乓球”课程的学生人数。

孔子曾说:“知之者不如好之者，好之者不如乐之者”兴趣是最好的老师。阅读、书法、绘画、手工、烹饪、运动、音乐…各种兴趣爱好是打开创新之门的金钥匙。某校为了解学生兴趣爱好情况，组织了问卷调查活动，从全校2200名学生中随机抽取了200人进行调查，其中一项调查内容是学生每周自主发展兴趣爱好的时长，对这项调查结果使用画“正”字的方法进行初步统计，得到下表:学生每周自主发展兴趣爱好时长分布统计表组别时长t(单位：h) 人数累计人数第一组 1≤t<2 正正正正正正 30第二组 2 正正正正正正正正正正正正 60第三组 3≤t<4 正正正正正正正正正正正正正正 70第四组 4 正正正正正正正正 40根据以上信息，解答下列问题:(1)全数分布直方图 (2)这200名学生每周自主发展兴趣爱好时长的中位数落在第______组;(3)若将上述调查结果绘制成扇形统计图，则第二组的学生人数占调查总人数的百分比为______，对应的扇形圆心角的度数为______。(4)学校倡议学生每周自主发展兴趣爱好时长应不少于2h，请你估计，该校学生中有多少人需要增加自主发展兴趣爱好时间?

为了解落实国家《关于全面加强新时代大中小学劳动教育的意见》的实施情况，某校从全体学生中随机抽取部分学生，调查他们平均每周劳动时间t(单位：h)，按劳动时间分为四组：A组“t<5”，B组“5≤t<7”，C组“7≤t<9”，D组“t≥9”.将收集的数据整理后，绘制成如下两幅不完整的统计图.平均每周劳动时间条形统计图平均每周劳动时间扇形统计图根据以上信息,解答下列问题：(1)这次抽样调查的样本容量是______，C组所在扇形的圆心角的大小是______；(2)将条形统计图补充完整；(3)该校共有1500名学生，请你估计该校平均每周劳动时间不少于7h的学生人数.

某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程，要求每人必须参加，并且只能选择其中一门课程.为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调査，并根据调査结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出). 请你根据以上信息解决下列问题：(1)参加问卷调查的学生人数为______名，补全条形统计图(画图并标注相应数据)；(2)在扇形统计图中，选择“陶艺”课程的学生占______%;(3)若该校八年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？

某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调查(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:(1)这次活动一共调查了______名学生;(2)在扇形统计图中,“其他”所在扇形圆心角等于______度(3)补全条形统计图;(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是______人.

为了了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况，随机抽查了部分参赛同学的成绩，整理并制作图表如下：分数段频数频率60≤x<70 30 0.170≤x<80 90 n80≤x<90 m 0.490≤x<100 60 0.2根据以上图表提供的信息，解答下列问题：(1)本次调查的样本容量为______；(2)在表中：m=______，n=______；(3)补全频数分布直方图； (4)参加比赛的小聪说，他的比赛成绩是所有抽查同学成绩的中位数，据此推断他的成绩落在__________分数段内；(5)如果比赛成绩80分以上（含80分）为优秀，那么你估计该竞赛项目的优秀率大约是________.

写有“中国”、“美国”、“英国”、“韩国”的四张卡片，从中随机抽取一张，抽到卡片所对应的国家为亚洲的概率是________.

解不等式组：，并写出其整数解.