初中数学-中考试题(山西省 2020年统计计算)

问答题（2020年山西省）

2020年国家提出并部署了“新基建”项目，主要包含“特高压，城际高速铁路和城市轨道交通，5G基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩”等．《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域（5G基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩）总体的人才与就业机会．下图是其中的一个统计图．

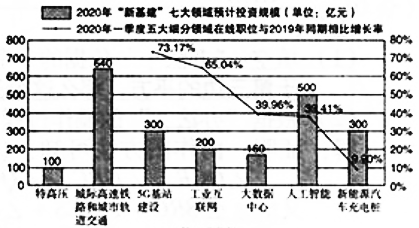
请根据图中信息，解答下列问题：

(1）填空：图中2020年“新基建”七大领域预计投资规模的中位数是______亿元；

(2）甲，乙两位待业人员，仅根据上面统计图中的数据，从五大细分领域中分别选择了“5G基站建设”和“人工智能”作为自己的就业方向，请简要说明他们选择就业方向的理由各是什么；

(3）小勇对“新基建”很感兴趣，他收集到了五大细分领域的图标，依次制成编号为W，G，D，R，X的五张卡片（除编号和内容外，其余完全相同），将这五张卡片背面朝上，洗匀放好，从中随机抽取一张（不放回），再从中随机抽取一张．请用列表或画树状图的方法求抽到的两张卡片恰好是编号为W（5G基站建设）和R（人工智能）的概率．

答案解析

（1）300（2）解：甲更关注在线职位增长率，在“新基建”五大细分领域中，2020年第一季度“5G基站建设”在线职位与2019年同期相比增长率最高；乙更关注预计投资规模，在“新基建”五大细分领域中，“人工智能”在2020年...

查看完整答案

讨论

初中数学

如图，四边形OABC是平行四边形，以点O为圆心，OC为半径的⊙O与AB相切于点B，与AO相交于点D，AO的延长线交⊙O于点E，连接EB交OC于点F，求∠C和∠E的度数．

2020年5月份，省城太原开展了“活力太原·乐购晋阳”消费暖心活动，本次活动中的家电消费券单笔交易满600元立减128元（每次只能使用一张）某品牌电饭煲按进价提高50%后标价，若按标价的八折销售，某顾客购买该电饭煲时，使用一张家电消费券后，又付现金568元．求该电饭煲的进价．

下面是小彬同学进行分式化简的过程，请认真阅读并完成相应任务．= 第一步= 第二步= 第三步= 第四步= 第五步= 第六步任务一：填空：①以上化简步骤中，第_____步是进行分式的通分，通分的依据是____________________或填为_____________________________；②第_____步开始出现错误，这一步错误的原因是_____________________________________；任务二：请直接写出该分式化简后的正确结果；任务三：除纠正上述错误外，请你根据平时的学习经验，就分式化简时还需要注意的事项给其他同学提一条建议．

计算：(-4)2×(-)3-(-4+1)

如图，在RtΔABC中，∠ACB=90°，AC=3，BC=4，CD⊥AB，垂足为D，E为BC的中点，AE与CD交于点F，则DF的长为_______．

如图是一张长12cm，宽10cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分（阴影部分）可制成底面积24cm2是的有盖的长方体铁盒．则剪去的正方形的边长为______cm．

某校为了选拔一名百米赛跑运动员参加市中学生运动会，组织了6次预选赛，其中甲，乙两名运动员较为突出，他们在6次预选赛中的成绩（单位：秒）如下表所示：甲 12.0 12.0 12.2 11.8 12.1 11.9乙 12.3 12.1 11.8 12.0 11.7 12.1由于甲，乙两名运动员的成绩的平均数相同，学校决定依据他们成绩的稳定性进行选拔，那么被选中的运动员是______．

如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形⋯按此规律摆下去，第n个图案有_______个三角形（用含n的代数式表示）．，，，，…

计算__________.

如图是一张矩形纸板，顺次连接各边中点得到菱形，再顺次连接菱形各边中点得到一个小矩形．将一个飞镖随机投掷到大矩形纸板上，则飞镖落在阴影区域的概率是【】

统计初步

随机调查某城市30天空气质量指数(AQI)，绘制成如下扇形统计图。空气质量等级空气质量指数(AQI) 频数优 AQI≤50 m良 50<AQI≤100 15中 100<AQI≤150 9差 AQI>150 n(1)m=_____,n=_____;(2)求良的占比;(3)求差的圆心角;(4)折线图是一个月内的空气污染指数统计，然后根据这个一个月内的统计进行估测一年的空气污染指数为中的天数，从折线图可以得到空气污染指数为中的有9天.根据折线统计图，一个月(30天)中有_____天AQI为中，估测该城市一年(以365天计)中大约有______天AQI为中.

为有效推进儿童青少年近视防控工作，教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案(2021-2025年)》，共提出八项主要任务，其中第三项任务为强化户外活动和体育锻炼，我市各校积极落实方案精神，某学校决定开设以下四种球类的户外体育选修课程：篮球、足球、排球、乒乓球，为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程)，并根据调查结果绘制成不完整的统计图表。根据图表信息，解答下列问题:(1)分别求出表中m，n的值;(2)求扇形统计图中“足球”对应的扇形圆心角的度数;(3)该校共有2000名学生，请你估计其中选择“乒乓球”课程的学生人数。

孔子曾说:“知之者不如好之者，好之者不如乐之者”兴趣是最好的老师。阅读、书法、绘画、手工、烹饪、运动、音乐…各种兴趣爱好是打开创新之门的金钥匙。某校为了解学生兴趣爱好情况，组织了问卷调查活动，从全校2200名学生中随机抽取了200人进行调查，其中一项调查内容是学生每周自主发展兴趣爱好的时长，对这项调查结果使用画“正”字的方法进行初步统计，得到下表:学生每周自主发展兴趣爱好时长分布统计表组别时长t(单位：h) 人数累计人数第一组 1≤t<2 正正正正正正 30第二组 2 正正正正正正正正正正正正 60第三组 3≤t<4 正正正正正正正正正正正正正正 70第四组 4 正正正正正正正正 40根据以上信息，解答下列问题:(1)全数分布直方图 (2)这200名学生每周自主发展兴趣爱好时长的中位数落在第______组;(3)若将上述调查结果绘制成扇形统计图，则第二组的学生人数占调查总人数的百分比为______，对应的扇形圆心角的度数为______。(4)学校倡议学生每周自主发展兴趣爱好时长应不少于2h，请你估计，该校学生中有多少人需要增加自主发展兴趣爱好时间?

2013 年起，深圳市实施行人闯红灯违法处罚，处罚方式分为四类:“罚款20元”、“罚款50元”、“罚款 100元”、“穿绿马甲维护交通”，如图是实施首日由某片区的执法结果整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题:(1)实施首日，该片区行人闯红灯违法受处罚一共______；(2)在所有闯红灯违法受处罚的行人中，穿绿马甲维护交通所占的百分比是______%；(3)据了解，“罚款20元”人数是“罚款50元”人数的2倍，请补全条形统计图；(4)根据(3)中的信息，在扇形统计图中，“罚款20元”所在扇形的圆心角等于______度.行人闯红灯违法处罚条形统计图行人闯红灯违法处罚扇形统计图

在-2，1，2，1，4，6中正确的是【】

关于体育选考项目统计图项目频数频率A 80 BB C 0.3C 20 0.1D 40 0.2合计 a 1(1)求出表中a,b,c的值，并将条形统计图补充完整.表中a=______，b=______，c=______. (2)如果有3万人参加体育选考，会有多少人选择篮球?

11月读书节，深圳市为统计某学校初三学生读书状况，如下图： (1)三本以上的x值为______，参加调查的总人数为______，补全统计图；(2)三本以上的圆心角为______；(3)全市有6.7万学生，三本以上有______人.

深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况，某校数学兴趣小组随机采访部分深圳市民，对采访情况制作了统计图表的一部分如下:关注情况频数频率A.高度关注 M 0.1B.一般关注 100 0.5C.不关注 30 ND.不知道 50 0.25东进战略关注情况条形统计图(1)根据上述统计图可得此次采访的人数为________人，M = ________，N = ________；(2)根据以上信息补全条形统计图；(3)根据上述采访结果，请估计在 15000 名深圳市民中，高度关注东进战略的深圳市民约有________人.

深圳市某学校抽样调查，A 类学生骑共享单车，B 类学生坐公交车、私家车等，C类学生步行，D类学生(其它)，根据调查结果绘制了不完整的统计图.类型频数频率A 30 xB 18 0.15C m 0.40D n y(1) 学生共______人，x=______，y=______；(2)补全条形统计图；(3)若该校共有 2000 人，骑共享单车的有______人.

某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形图：频数频率体育 40 0.4科技 25 a艺术 b 0.15其它 20 0.2请根据上图完成下面题目：(1)总人数为______人，a=______，b=______.(2)请你补充全条形统计图.(3)若全校有600人，请你估算一下全校喜欢艺术的学生人数有多少？

统计计算

在以下数据75，80，80，85，90中，众数、中位数分别是【】

某共享单车前a 公里1元，超过a 公里的，每公里2元，若要使使用该共享单车50%的人只花1元钱，a应该要取什么数【】

一组数据20,21,22,23,23的中位数和众数分别是【】

某市在实施居民用水定额管理前，对居民生活用水情况进行了调查，通过简单随机抽样，获得了100个家庭去年的月均用水量数据，将这组数据按从小到大的顺序排列，其中部分数据如下表:(1)求这组数据的中位数.已知这组数据的平均数为9.2t，你对它与中位数的差异有什么看法?(2)为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使75%的家庭水费支出不受影响，你觉得这个标准应该定为多少?

某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下:3，5，3，6，3，4，4，5，2，4，5，6，1，3，5，5，4，4，2，4根据以上数据，得到如下不完整的频数分布表:次数 1 2 3 4 5 6人数 1 2 a 6 b 2(1)表格中的a=______, b=______;(2)在这次调查中，参加志愿者活动的次数的众数为______，中位数为______;(3)若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数.

有甲、乙两组数据，如下表所示：甲 11 12 13 14 15乙 12 12 13 14 14甲、乙两组数据的方差分别为S甲2,S乙2则S甲2 ___ S乙2(填“>”，“<”或“=”)。

为了解甲、乙两座城市的邮政企业4月份收入的情况，从这两座城市的邮政企业中，各随机抽取了25家邮政企业，获得了它们4月份收入(单位：百万元)的数据，并对数据进行整理、描述和分析，下面给出了部分信息：a.甲城市邮政企业4月份收入的数据的频数分布直方图如下：数据分成5组：6≤x<8,8≤x<10,10≤x<12,12≤x<14,14≤x≤16. b.甲城市邮政企业4月份收入的数据在10≤x<12，这一组的数据是：10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8.c.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下: 平均数中位数甲城市 10.8 m乙城市 11.0 11.5根据以上信息，回答下列问题：(1).写出表中m的值:(2).在甲城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为p1，在乙城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为p2.比较p1,p2的大小，并说明理由:(3).若乙城市共有200家邮政企业，估计乙城市的邮政企业4月份的总收入(直接写出结果).

菲尔兹奖是数学领域的一项国际大奖，常被视为数学界的诺贝尔奖，每四年颁发一次，最近一届获奖者获奖时的年龄（单位：岁）分别为：30，40，34，36，则这组数据的中位数是【】

在读书节活动中，某校为了解学生参加活动的情况，随机调查了部分学生每人参加活动的项数.根据统计的结果，绘制出如下的统计图①和图② 请根据相关信息，解答下列问题:(1)本次接受调查的学生人数为______，图①中m的值为________；(Ⅱ)求统计的这组项数数据的平均数、众数和中位数.

五名同学捐款数分别是5，3，6，5，10(单位:元)，捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比，集中趋势相同的是【】