-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【点睛】本题考查的是正六边形的性质、等边三角形的判定与性质、勾股定理,熟练掌握正六边形的性质，由勾股定理求出OM 是解决问题的关键．
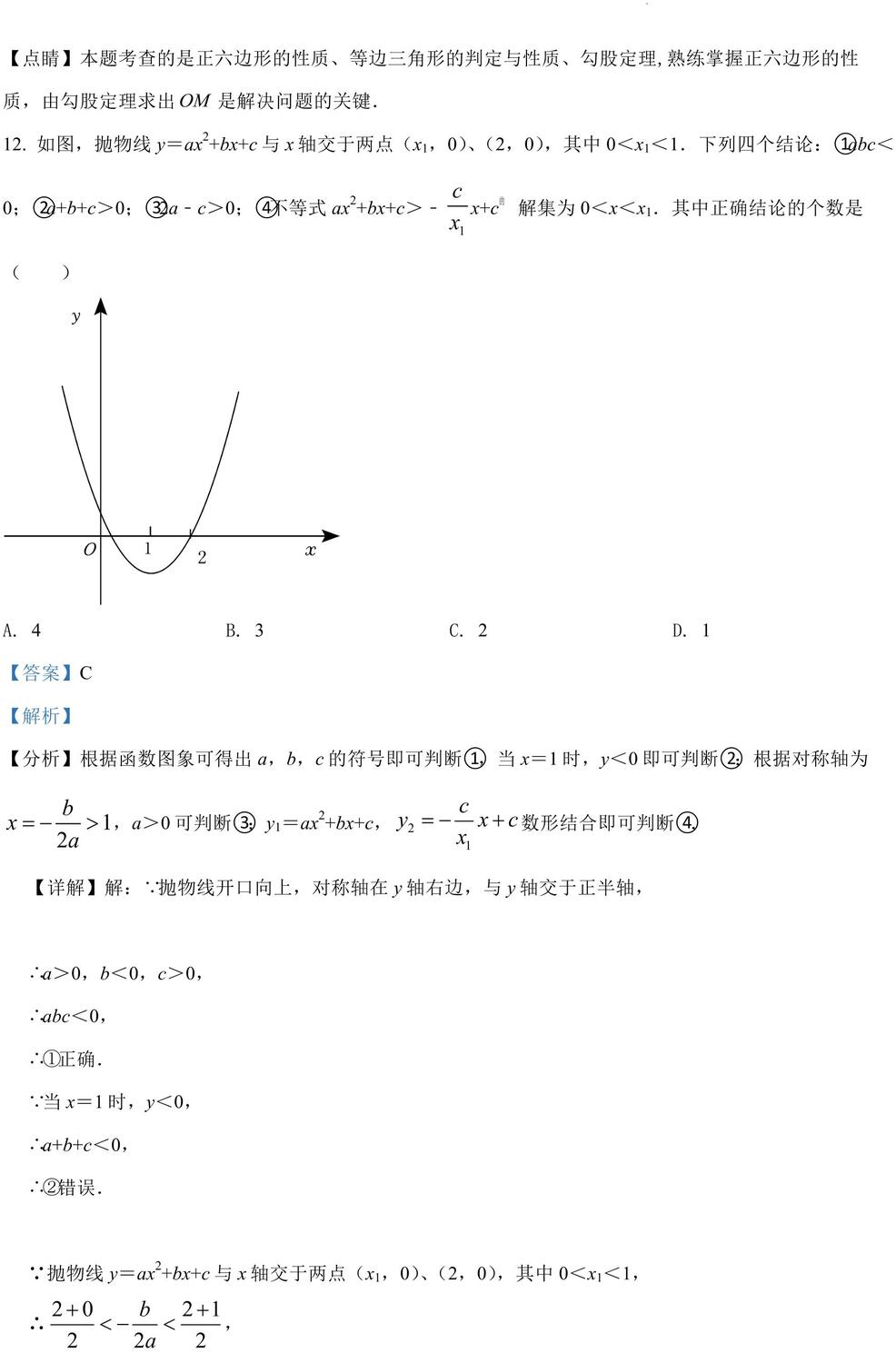
12. 如图，抛物线 y＝ax2+bx+c 与 x 轴交于两点（x1，0）、（2，0），其中 0＜x1＜1．下列四个结论：①abc＜
0；②a+b+c＞0；③2a﹣c＞0；④不等式 ax2+bx+c＞﹣
x+c 解集为 0＜x＜x1．其中正确结论的个数是
【分析】根据函数图象可得出 a，b，c 的符号即可判断①，当 x＝1 时，y＜0 即可判断②；根据对称轴为
= - > ，a＞0 可判断③；y1＝ax2+bx+c， 2
= - + 数形结合即可判断④．
【详解】解：∵抛物线开口向上，对称轴在 y 轴右边，与 y 轴交于正半轴，
∴①正确．
∵当 x＝1 时，y＜0，
∴②错误．
∵抛物线 y＝ax2+bx+c 与 x 轴交于两点（x1，0）、（2，0），其中 0＜x1＜1，