-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【分析】（1）连接 OD，只要证明 OD⊥DE即可；
（2）连接 CF，证 OD 是△ABC 的中位线，得 CF=2DE，再证 DE 是△FBC 的中位线，得
CF=2DE,设 AE=2x，DE=3k，则 CF=6k，BE=EF=AE+AF=2k+10，AC=BA=EF+AE=4k+10，然后在 Rt△ACF 中，由勾股定理，得 (4k+10)2=102+(6k)2， 解得：k=4，从而求得 AC=4k+10=4×4+10=26，即可求得 的半径 OA 长，即可求解．
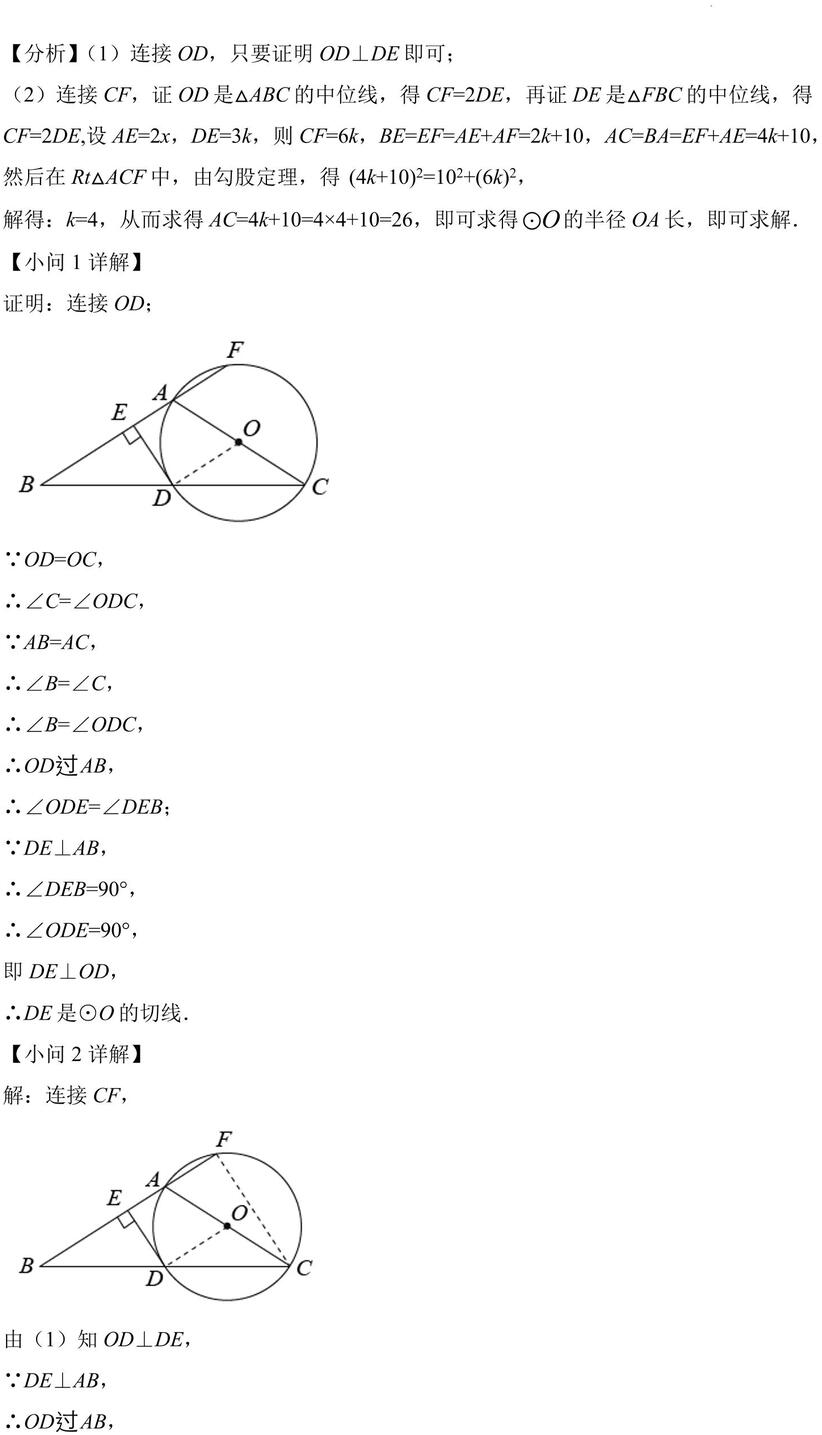
【小问 1详解】 证明：连接 OD； 即 DE⊥OD，
∴DE 是⊙O 的切线．
【小问 2详解】 解：连接 CF， 由（1）知 OD⊥DE，