一、学习目标

1.掌握绝对值的概念；

2.学会绝对值的计算；

3.有理数大小比较法则，会比较两个或多个有理数的大小；

4.体验数形结合的解题思想。

二、学习难点

两个负数大小的比较

三、知识重点

绝对值的概念

三、知识内容

1.绝对值的代数定义：

一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，零的绝对值是零。

2.绝对值的几何定义：

在数轴上表示一个数的点离开原点的距离，叫做这个数的绝对值。

3.绝对值的主要性质：

(1)一个实数的绝对值是一个非负数，即a≥0，因此，在实数范围内，绝对值最小的数是零；

(2)两个相反数的绝对值相等；

(3)三角不等式：|a|+|b|≥|a+b|。

4.运用绝对值比较有理数的大小

(1)两个负数大小的比较：

①先分别求出两个负数的绝对值；

②比较这两个绝对值的大小；

③根据“两个负数，绝对值大的反而小”作出正确的判断

(2)两个正数大小的比较：绝对值大的较大。

(3)一正一负的比较：正数大于负数。

四、中考解读

近年来，绝对值在全国各省市的中考试卷中出现频率较高，出题形式主要有以下几类：

1、与相反数隔年交替以选择题的形式出现，一般在试卷的第1、2题，具有引导考生放松心情、适应考场的用意，中考可能性：50%；

2、数形结合，在数轴上给出相关数字（或字母），比较大小或分析最值，中考可能性：40%；

3、利用绝对值的性质解题，在综合分析题或计算题中，利用绝对值的非负性确定未知数的值，中考可能性：10%；

4、分析绝对值的范围，利用绝对值不等式解题，中考可能性：5%，竞赛可能性：40%。

五、解题指导

1、由数求绝对值，由绝对值求数

解题技巧:

(1)由数求绝对值：|a|一定为非负数，即

(2)由绝对值求数

①绝对值为0 的数仅有1个，即 0； 绝对值为正数的数有2个，其为相反数；绝对值为负的数不存在。

②绝对值相等的两个数，可能相等，也可能互为相反数(使用数形结合法：使用数轴区分，可能会有多解)。

真题回放：

【2019年·湖北省黄冈市】-3的绝对值是【 】

A.-3    B.-1/3    C.3    D.±3

【答案】C

【分析】根据绝对值的定义直接进行计算。

2、有理数的大小比较

性质：

(1)在数轴上从左往右的顺序，数字依次增大；

(2)两个负数比较大小，绝对值大的反而小。

解题技巧：

(1)正数与正数比较，绝对值大者较大；

(2)正数与负数比较，正数>0>负数；

(3)负数与负数比较，绝对值大的反而小；

(4)如果要比较的数比较多，可在数轴上将每个数表示出来，在数抽上，从左至右，数值一次增大；

(5)当有字母时，且暂时无法理清大小关系，可以用特值法进行比较。

真题回放：

【2016年·北京市】实数a,b在数轴上的对应点的位置如图所示，则正确的结论是【 】

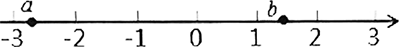
A. a>-2    B. a<-3    C. a>-b    D. a<-b

解题思路：根据数轴上a、b所在的位置，可得a和-b的取值范围，进而得出答案。

解题过程：如图所示，-3<a<-2，故此选项A、B错误；

如图所示，1<b<2，则-2<-b<-1，故a<-b，所以，C错，D对。

应试技巧：应答选择题时，如果选项中存在互斥（矛盾）的情况，则互斥的选项中必有一个为正解。进一步，在单项选择题中，该正解即为题目的唯一解。

本题中，选项C和D是互斥（矛盾）的，所以只分析C、D两项即可快速答题。

3、利用绝对值的非负性

性质：非负性即 |a|≥0（a为任意实数）。

解题技巧：此类题型往往出题为几个非负数相加，结果为 0，则这每个非负数必须为零。

真题回放：

【2009年·全国初中数学联赛】如果实数a、b满足条件

a²+b²=1，|1-2a+b|+2a+1=b²-a²，

则a+b=______.

解题思路：通过已条件挖掘1-2a+b的正负，从而去掉绝对值符号得以求解.

解答过程：

由a²+b²=1得：b²=1-a²，且-1≤a≤1,-1≤b≤1.

由|1-2a+b|=b²-a²得：

|1-2a+b|=b²-a²-2a-1

=(1-a²)-a²-2a-1

=-2a²-2a

从而，-2a²-2a≥0⇒-1≤a≤0.

故1-2a+b≥0,

因此，1-2a+b=-2a²-2a，即

1+b=-2a²=-2(1-b²)，整理得2b²-b-3=0，

解得b=-1（另一根舍去）.

把b=-1代入1+b=-2a²中，得a=0，

所以 a+b=-1.

4、化简含绝对值的代数式

(1)判断绝对值符号里式子的正负：

两数相减：大数-小数>0，转化到数轴上：右-左>0；小数-大数<0，转化到数轴上：左-右<0。

两数相加：正数+正数>0，转化到数轴上：原点右侧两数相加>0；负数+负数<0，转化到数轴上：原点左侧两数相加<0。

正数+负数：取绝对值较大数的符号，转化到数轴上：原点两侧两数相加，取离原点远的符号。

(2)将绝对值符号改为小括号：

若是正数，绝对值前的正负号不变（即本身）； 若是负数，绝对值前的正负号改变（即相反数）。

(3)去括号：括号前是“+”，去括号，括号内不变；括号前是“-”，去括号，括号内各项要变号。

(4)化简代数式

真题回放：

【1999年·希望杯】有理数a、b、c在数轴上的位置如图所示.则化简|a+b|-|b-1|-|a-c|-|1-c|所得的结果是______.

解答：由题意可得，a+b<0,b-1<0,a-c<0,1-c>0.

∴原式=-(a+b)-[-(b-1)]-[-(a-c)]-(1-c)

=-a-b+b-1+a-c-1+c

=-2