对下图所示的二叉树进行中序遍历(左子树、根结点、右子树)的结果是【 】。
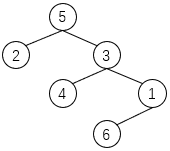
A、5 2 3 4 6 1
B、2 5 3 4 1 6
C、2 4 6 5 3 1
D、2 5 4 3 6 1
对下图所示的二叉树进行中序遍历(左子树、根结点、右子树)的结果是【 】。

A、5 2 3 4 6 1
B、2 5 3 4 1 6
C、2 4 6 5 3 1
D、2 5 4 3 6 1
D
如果只考虑有序树的情形,那么具有7个结点的不同形态的树共有【】
已知一棵度为m的树中有N1个度为1的结点,N2个度为2的结点,...,Nm个度为m的结点。试问该树中有多少个叶子结点?
某二又树的先序遍历序列为 ABCDFGE,中序遍历序列为 BAFDGCE。以下关于该二又树的叙述中,正确的是【 】。
算术表达式a+(b-c)*d的后缀式是【 】(-、+、*表示算术的减、加、乘运算,运算符的优先级和结合性遵循惯例)。
在解决计算机与打印机之间速度不匹配的问题时,通常设置一个打印数据缓冲区,计算机将要输出的数据依次写入该缓冲区,而打印机则依次从该缓冲区取出数据。因此,该缓冲区的数据结构应该是【 】。
若元素a、b、c、d、e、f依次进栈,允许进栈、出栈操作交替进行。但不允许连续三次进行出栈工作,则不可能得到的出栈序列是【 】。