证 明 题(高等数学·2004年·重庆大学)
已知A ̅和B ̅分别是三维空间中的矢量矩阵和单位方向矢量;
A ̅=Ax +Ay
+Ay +Az
+Az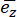 ;( Ax=
;( Ax= ,Ay=
,Ay=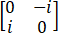 ,Az=
,Az=
B ̅=cosα +cosβ
+cosβ +cosγ
+cosγ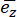 ;( cos2 α+cos2 β+cos2 γ=1)
;( cos2 α+cos2 β+cos2 γ=1)
计算矩阵求和c=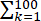 k(A ̅∙B ̅)k +
k(A ̅∙B ̅)k +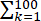 2k (A ̅∙B ̅)2k.
2k (A ̅∙B ̅)2k.
提示:首先考察(A ̅∙B ̅)2=?
解答提示
暂无答案
已知α1=,α2=,α3=,记β1=α1,β2=α2 - kβ1,β3=α3 - l1 β1 - l2 β2,若β1,β2,β3 两两正交,则l1,l2依次为【 】
设A是n×n实对称矩阵,证明:存在一个实数k使得对任意一个实n维向量x都有|x' Ax|≤kx'x,其中x'表示向量x的转置.
设对角矩阵A的特征多项式为 φ(λ)=(λ-λi)ni (诸λi两两互异),求所有和A可交换的矩阵全体所组成的线性空间的维数.
用数学归纳法证明:对于复n维空间Vn上任意多个两两可交换的线性变换所组成的集合S具有公共的特征向量.
已知四维实矢量空间的矢量(表示成矩阵):=,满足如下条件:以及T∙=9/4(其中,T表示对矩阵取置换),试求出所有这样的四维实矢量的集合:{ }=?

