单项选择（数学·2020年3月·阿里巴巴）

面条是中华传统美食，花样不断翻新。清晨，擀宽面的张师傅别出心裁，把他的宽面条两头粘上，变成了宽面圈儿，如图：

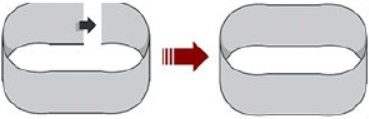
他平时切面条一样，把宽面圈儿沿着中心线切开，就得到两个完全同样的宽面圈儿，如图：

张师傅灵机一动，重新将面条拧了一下，再两头粘上。这样竟然成了数学中常常讲到的莫比乌斯带（以德国数学家奥古斯特●莫比乌斯命名），如图：

接着，他灵机两动，三动，直至n动。将宽面拧了两个，三下，直至n下，总以如图的右手内旋的方式来拧，然后照样地两头粘上。这些宽面圈儿在数学上还没有固定的名称。张师傅把莫比乌斯带称作1旋圈面，拧两下、三下的称作2旋、3旋圈面，总之，拧n下就是旋圈面；n为2、3、7的情形如图：

起先没有拧就粘上的，普普通通，只称作平凡圈面，或者0旋圈面。在线师傅看来，不同旋数的圈面是彼此不同的（因为只在厨房里摆放来，摆放去，总不能把一种变成另一种）。

张师傅把他的多旋圈面开店上架，一时网红。有人为百岁老人订制100旋圈面，有人为公司年会订制2019旋圈面，（张师傅拧得手都酸了）。试问：张师傅要是依旧沿中心线切开这两种圈面，分别会得到什么？【 】

A、一个200旋圈面，一个非上述构造的圈面

B、两个100旋圈面，一个非上述构造的圈面

C、一个200旋圈面，一个0旋圈面

D、两个100旋圈面，一个0旋圈面

解答提示

B对于了解扭结理论的读者，如下描述也许最为直截了当：三维空间中嵌入的平环，沿中心线切开总给出与原先同痕的两个平环；而嵌入的莫比乌斯带，如果中心线不打结的话，切开会给出一个嵌入平环，且平环的中心线通常打结（除了图3及其镜像，中心线都是非平凡的环面结）明白这个描述，就能立即推断正确的选项应为“两个100旋圈面，一个非上述构造的圈面”.如果读者不熟悉这些术语，更有效的办法就是动手试试剪开n旋圈面（纸带），比方说，n等于1，2，3，4等等.不多的几次尝试就容易归纳出，偶数n旋的圈面切开总是会给出两个圈面.如果把它们每个的宽度拉伸到两倍，那么每个都全等于切开前的圈面.所以，100旋圈面切开就是两个100旋圈面.奇数n旋圈面切开总给出仅仅一个圈面.观察纸带模型，我们可以说，这反映了奇数旋圈面只有1条边界：矩形纸带的左边颠倒粘在右边，那么上边的尾接到下边的头，下尾又接到上头.切开后的圈面有两条边界，一条原来的，一条由切开产生.新的中心线平行于...

查看完整答案，请下载word版