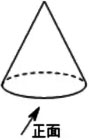
如图所示的圆锥,下列说法正确的是【 】
A、该圆锥的主视图是轴对称图形
B、该圆锥的主视图是中心对称图形
C、该圆锥的主视图既是轴对称图形,又是中心对称图形
D、该圆锥的主视图既不是轴对称图形,又不是中心对称图形
如图所示的圆锥,下列说法正确的是【 】

A、该圆锥的主视图是轴对称图形
B、该圆锥的主视图是中心对称图形
C、该圆锥的主视图既是轴对称图形,又是中心对称图形
D、该圆锥的主视图既不是轴对称图形,又不是中心对称图形
A
【解析】
圆锥的主视图是等腰三角形,是轴对称图形,不是中心对称图形.