初中数学-中考试题(广东省广州市 2022年统计计算)

问答题（2022年广东省广州市）

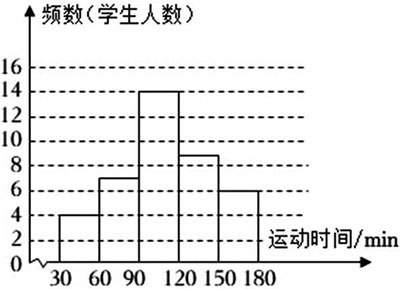
某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图.

频数分布表

运动时间t/min 频数频率

30≤t<60 4 0.1

60≤t<90 7 0.175

90≤t<120 a 0.35

120≤t<150 9 0.225

150≤t<180 6 b

合计 n 1

频数分布直方图

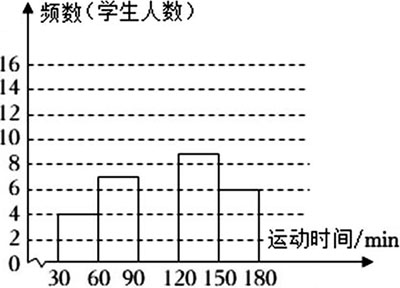
请根据图表中的信息解答下列问题：

(1)频数分布表中的a=_____,b=______,n=______；

(2)请补全频数分布直方图;

(3)若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数.

答案解析

(1)由题意可知：n=4÷0.1=40,

∴a=40×0.35=14,b=6÷40=0.15.

(2)补全步数直方图如下：

(3)480×(9+6)/40=180(人).

讨论

统计初步

我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了【】

小红家到学校有两条公共汽车线路。为了解两条线路的乘车所用时间，小红做了试验，第一周(5个工作日)选择A线路，第二周(5个工作日)选择B线路，每天在固定时间段内乘车2次并分别记录所用时间，数据统计如下:(单位: min)数据统计表实验序号 1 2 3 4 5 6 7 8 9 10A线路所用时间 15 32 15 16 34 18 21 14 35 20B线路所用时间 25 29 23 25 27 26 31 28 30 24根据以上信息解答下列问题平均数中位数众数方差A线路所用时间 22 a 15 63.2B线路所用时间 b 26.5 c 6.36(1)填空：a=________；b=________；c=________；(2)应用你所学的统计知识，帮助小红分析如何选择乘车线路.数据拆线统计图

为振兴乡村经济，在农产品网络销售中实行目标管理，根据目标完成的情况对销售员给予适当的奖励，某村委会统计了15名销售员在某月的销售额(单位:万元)，数据如下：10，4，7，5，4，10，5，4，4，18，8，3，5，10，8.(1)补全月销售额数据的条形统计图.(2)月销售额在哪个值的人数最多(众数)?中间的月销售额(中位数)是多少?均月销售额(平数)是多少?(3)根据(2)中的结果，确定一个较高的销售目标给予奖励，你认为月销售额定为多少合适?

下表为五种运动耗氧情况，其中耗氧量的中位数是【】打网球跳绳爬楼梯慢跑游泳80L/h 90L/h 105L/h 110L/h 115L/h

为了提高某城区居民的生活质量，政府将改造城区配套设施，并随机向某居民小区发放调查问卷(1人只能投1票)，共有休闲设施，儿童设施，娱乐设施，健身设施4种选项，一共调查了 a 人，其调查结果如下：如图，为根据调查结果绘制的扇形统计图(图1)和条形统计图(图 2)，请根据统计图回答下面的问题：① 总人数a=________人；② 请补充条形统计图；③ 若该城区共有10万居民，则其中愿意改造“娱乐设施”的约有多少人？④ 改造完成后，该政府部门向甲、乙两小区下发满意度调查问卷，其结果(分数)如下：项目小区休闲儿童娱乐健身甲 7 7 9 8乙 8 8 7 9若以1:1:1:1进行考核，______小区满意度（分数）更高；若以1:1:2:1进行考核，______小区满意度（分数）更高.

某校为了了解学生对中国民族乐器的喜爱情况，随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器)，现将收集到的数据绘制成如下两幅不完整的统计图.(1)这次共抽取______名学生进行调查，扇形统计图中的x=______；(2)请补全统计图；(3)在扇形统计图中“扬琴”所对扇形的圆心角是______度；(4)若该校有3000名学生，请你估计该校喜爱“二胡”的学生约有______名.

某同学在今年的中考体育测试中选考跳绳，考前一周，他记录了自己五次跳绳的成绩(次数/分钟)：247,253,247,255，263.这五次成绩的平均数和中位数分别是【】

以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业态发展对人才的需求更加旺盛。某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生，现随机调查了m名新聘毕业生的专业情况，并将调查结果绘制成如图两幅不完整的统计图. 请根据统计图提供的信息，解答下列问题.(1)m=______，n=______.(2)请补全条形统计图；(3)在扇形统计图中，“软件”所对应的扇形的圆心角是______度；(4)若该公司新招聘600名毕业生，请你估计“总线”专业的毕业生有______名.

某学校进行演讲比赛，最终有7位同学进入决赛，这七位同学的评分分别是：9.5，9.3，9.1，9.4，9.7，9.3，9.6.请问这组评分的众数是【】

某工厂一共有1200人，为选拔人才，提出了一些选拔的条件，并进行了抽样调查。从中抽出400人，发现有300人是符合条件的，那么则该工厂1200人中符合选拔条件的人数为______人.

统计计算

某洗车公司安装了A,B两款自动洗车设备，工作人员从消费者对A,B两款设备的满意度评分中各随机抽取20份，并对数据进行整理、描述和分析(评分分数用x表示，分为四个等级：不满意x<70，比较满意70≤x<80，满意80≤x<90，非常满意x≥90)，下面给出了部分信息：抽取的对A款设备的评分数据中“满意”包含的所有数据：83,85,85,87,89 抽取的对B款设备的评分数据：68,69,76,78,81,84,85,86,87,87,87,89,95,97,98,98,98,98,99,100.抽取的对A,B款设备的评分统计表：设备平均数中位数众数 “非常满意”占比A 88 m 96 45%B 88 87 n 40%根据以上信息，解答下列问题：(1)填空：a=______,m=______，n=______；(2)5月份，有600名消费者对A款自动洗车设备进行评分，估计其中对A款自动洗车设备“比较满意”的人数；(3)根据以上数据，你认为哪一款自动洗车设备更受消费者欢迎？请说明理由（写出一条即可）.

数据1、2、5、3、5、3、3的中位数是【】

某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况（每位同学必须且只能选择最喜爱的一项运动项目），进行了随机抽样调查，并将调查结果统计后绘制成了如下表和下图所示的不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图； (2)若七年级学生总人数为920人，请你估计七年级学生喜爱羽毛球运动项目的人数.

某高校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图． (1)这次被调查的同学共有________名；(2)把条形统计图补充完整；(3)校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校18 000名学生一餐浪费的食物可供多少人食用一餐？

一组数据2，6，5，2，4，则这组数据的中位数是【】

某公司的拓展部有五个员工,他们每月的工资分别是3000元，4000元，5000元，7000元和10000元，那么他们工资的中位数是【】

某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球，乒乓球，篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育项目的学生人数，随机抽取了部分学生进行调查，并将通过点差获得的数据进行整理，绘制出以下两幅不完整的统计图.请根据统计图回答问题：(1)这次活动一共调查了 250 名学生；(2)补全条形统计图；(3)在扇形统计图中，选择篮球项目的人数所在扇形的圆心角等于108度；(4)若该学校有1500人，请你估计该学校选择足球项目的学生人数约是480人.

在学校举行“阳光少年，励志青春”的演讲比赛中，五位评委给选手小明的评分分别为：90，85，90，80，95，则这组数据的众数是【】

某校为了解九年级学生的体重情况，随机抽取了九年级部分学生进行调查，将抽取学生的体重情况绘制如下不完整的统计图表，如图表所示，请根据图表信息回答下列问题：体重频数分布表组边体重（千克）人数A 45≤x＜50 12B 50≤x＜55 mC 55≤x＜60 80D 60≤x＜65 40E 65≤x＜70 16(1)填空：①m=______（直接写出结果）；②在扇形统计图中，C组所在扇形的圆心角的度数等于______度；(2)如果该校九年级有1000名学生，请估算九年级体重低于60千克的学生大约有多少人？

数据1、5、7、4、8的中位数是【】

数据处理

某工厂进行厂长选拔，从中抽出一部分人进行筛选，其中有“优秀”，“良好”，“合格”，“不合格”. (1)本次抽查总人数为________，“合格”人数的百分比为________.(2)补全条形统计图.(3)扇形统计图中“不合格人数”的度数为________.(4)在“优秀”中有甲乙丙三人，现从中抽出两人，则刚好抽中甲乙两人的概率为________.

2023年5月30日是第7个全国科技工作者日，某中学举行了科普知识手抄报评比活动，共有100件作品获得一、二、三等奖和优胜奖，则a的值为______.若将获奖作品按四个等级所占比例绘制成扇形统计图，则“一等奖”对应扇形的圆心角度数为______°.

为了解公园用地面积x(单位：公顷)的基本情况，某地随机调查了本地50个公园的用地面积，按照0<x≤4，4<x≤8，8<x≤12，12<x≤16，16<x≤20的分组绘制了如图所示的频数分布直方图，下列说法正确的是【】

某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调查(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:(1)这次活动一共调查了______名学生;(2)在扇形统计图中,“其他”所在扇形圆心角等于______度(3)补全条形统计图;(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是______人.

为了了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况，随机抽查了部分参赛同学的成绩，整理并制作图表如下：分数段频数频率60≤x<70 30 0.170≤x<80 90 n80≤x<90 m 0.490≤x<100 60 0.2根据以上图表提供的信息，解答下列问题：(1)本次调查的样本容量为______；(2)在表中：m=______，n=______；(3)补全频数分布直方图； (4)参加比赛的小聪说，他的比赛成绩是所有抽查同学成绩的中位数，据此推断他的成绩落在__________分数段内；(5)如果比赛成绩80分以上（含80分）为优秀，那么你估计该竞赛项目的优秀率大约是________.

为了解落实国家《关于全面加强新时代大中小学劳动教育的意见》的实施情况，某校从全体学生中随机抽取部分学生，调查他们平均每周劳动时间t(单位：h)，按劳动时间分为四组：A组“t<5”，B组“5≤t<7”，C组“7≤t<9”，D组“t≥9”.将收集的数据整理后，绘制成如下两幅不完整的统计图.平均每周劳动时间条形统计图平均每周劳动时间扇形统计图根据以上信息,解答下列问题：(1)这次抽样调查的样本容量是______，C组所在扇形的圆心角的大小是______；(2)将条形统计图补充完整；(3)该校共有1500名学生，请你估计该校平均每周劳动时间不少于7h的学生人数.

某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程，要求每人必须参加，并且只能选择其中一门课程.为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调査，并根据调査结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出). 请你根据以上信息解决下列问题：(1)参加问卷调查的学生人数为______名，补全条形统计图(画图并标注相应数据)；(2)在扇形统计图中，选择“陶艺”课程的学生占______%;(3)若该校八年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？

随机调查某城市30天空气质量指数(AQI)，绘制成如下扇形统计图。空气质量等级空气质量指数(AQI) 频数优 AQI≤50 m良 50<AQI≤100 15中 100<AQI≤150 9差 AQI>150 n(1)m=_____,n=_____;(2)求良的占比;(3)求差的圆心角;(4)折线图是一个月内的空气污染指数统计，然后根据这个一个月内的统计进行估测一年的空气污染指数为中的天数，从折线图可以得到空气污染指数为中的有9天.根据折线统计图，一个月(30天)中有_____天AQI为中，估测该城市一年(以365天计)中大约有______天AQI为中.

为有效推进儿童青少年近视防控工作，教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案(2021-2025年)》，共提出八项主要任务，其中第三项任务为强化户外活动和体育锻炼，我市各校积极落实方案精神，某学校决定开设以下四种球类的户外体育选修课程：篮球、足球、排球、乒乓球，为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程)，并根据调查结果绘制成不完整的统计图表。根据图表信息，解答下列问题:(1)分别求出表中m，n的值;(2)求扇形统计图中“足球”对应的扇形圆心角的度数;(3)该校共有2000名学生，请你估计其中选择“乒乓球”课程的学生人数。

孔子曾说:“知之者不如好之者，好之者不如乐之者”兴趣是最好的老师。阅读、书法、绘画、手工、烹饪、运动、音乐…各种兴趣爱好是打开创新之门的金钥匙。某校为了解学生兴趣爱好情况，组织了问卷调查活动，从全校2200名学生中随机抽取了200人进行调查，其中一项调查内容是学生每周自主发展兴趣爱好的时长，对这项调查结果使用画“正”字的方法进行初步统计，得到下表:学生每周自主发展兴趣爱好时长分布统计表组别时长t(单位：h) 人数累计人数第一组 1≤t<2 正正正正正正 30第二组 2 正正正正正正正正正正正正 60第三组 3≤t<4 正正正正正正正正正正正正正正 70第四组 4 正正正正正正正正 40根据以上信息，解答下列问题:(1)全数分布直方图 (2)这200名学生每周自主发展兴趣爱好时长的中位数落在第______组;(3)若将上述调查结果绘制成扇形统计图，则第二组的学生人数占调查总人数的百分比为______，对应的扇形圆心角的度数为______。(4)学校倡议学生每周自主发展兴趣爱好时长应不少于2h，请你估计，该校学生中有多少人需要增加自主发展兴趣爱好时间?