-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
关键是能得出含字母的式子表达抛物线平移后的解析式．
24. 小东在做九上课本 123页习题：“1： 也是一个很有趣的比．已知线段 AB（如图
1），用直尺和圆规作 AB 上的一点 P，使 AP：AB＝1： ．”小东的作法是：如图 2，以
AB 为斜边作等腰直角三角形 ABC，再以点 A 为圆心，AC 长为半径作弧，交线段 AB 于点
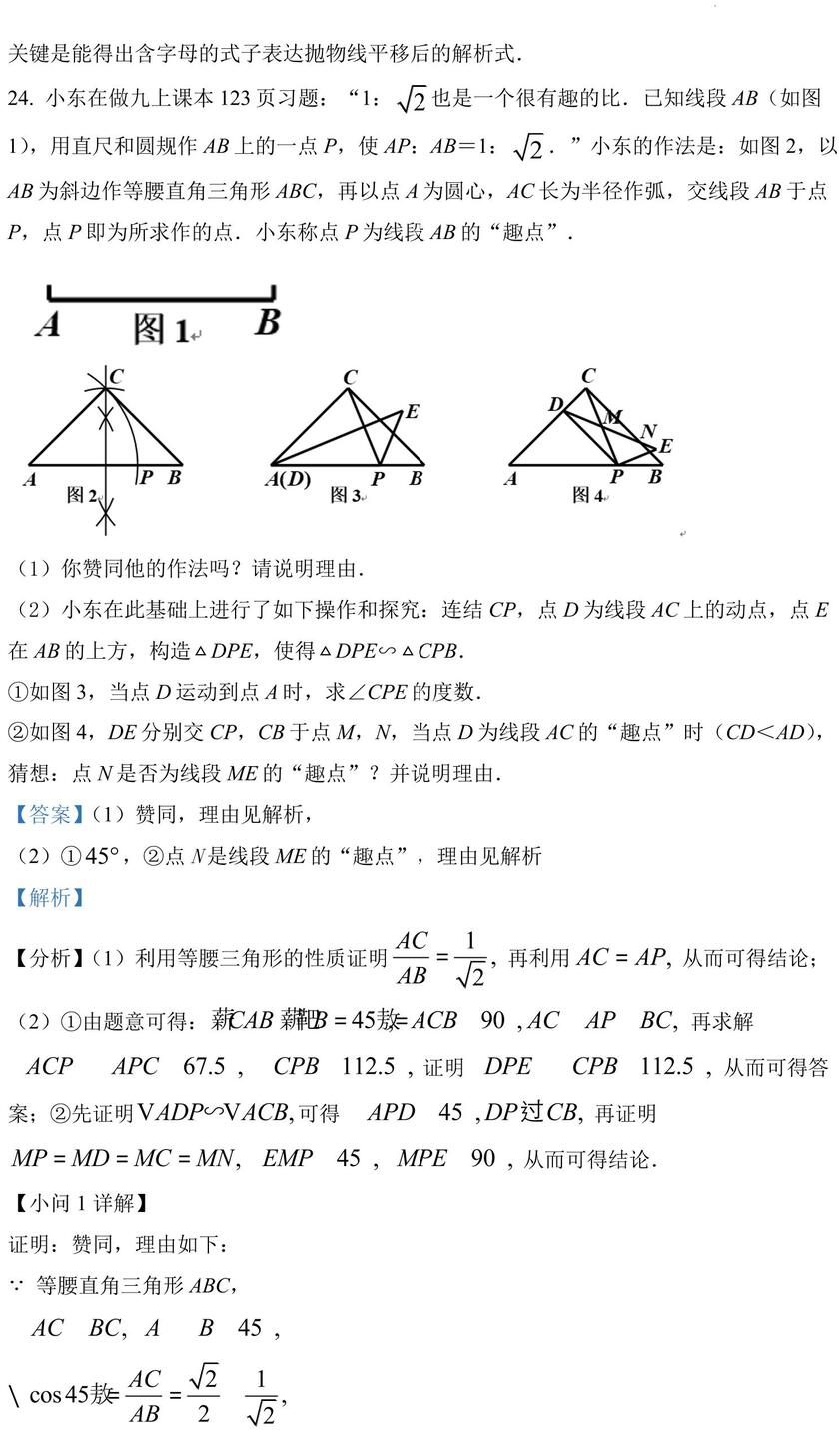
P，点 P即为所求作的点．小东称点 P 为线段 AB 的“趣点”．
（1）你赞同他的作法吗？请说明理由．
（2）小东在此基础上进行了如下操作和探究：连结 CP，点 D 为线段 AC 上的动点，点 E在 AB 的上方，构造 DPE，使得 DPE∽ CPB．
①如图 3，当点 D 运动到点 A 时，求∠CPE 的度数．
②如图 4，DE 分别交 CP，CB 于点 M，N，当点 D 为线段 AC 的“趣点”时（CD＜AD），猜想：点 N 是否为线段ME 的“趣点”？并说明理由．
【答案】（1）赞同，理由见解析，
（2）① ，②点 N是线段ME 的“趣点”，理由见解析
【分析】（1）利用等腰三角形的性质证明 再利用 从而可得结论；
（2）①由题意可得： 再求解
证明 从而可得答案；②先证明 可得 再证明
从而可得结论．
【小问 1详解】 证明：赞同，理由如下：
等腰直角三角形 ABC，
45 , 90 , ,CAB B ACB AC AP BC薪 薪靶 = 敖=
敖= =