-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【点睛】本题主要考查解解直角三角形，熟练掌握三角函数是解题的关键．
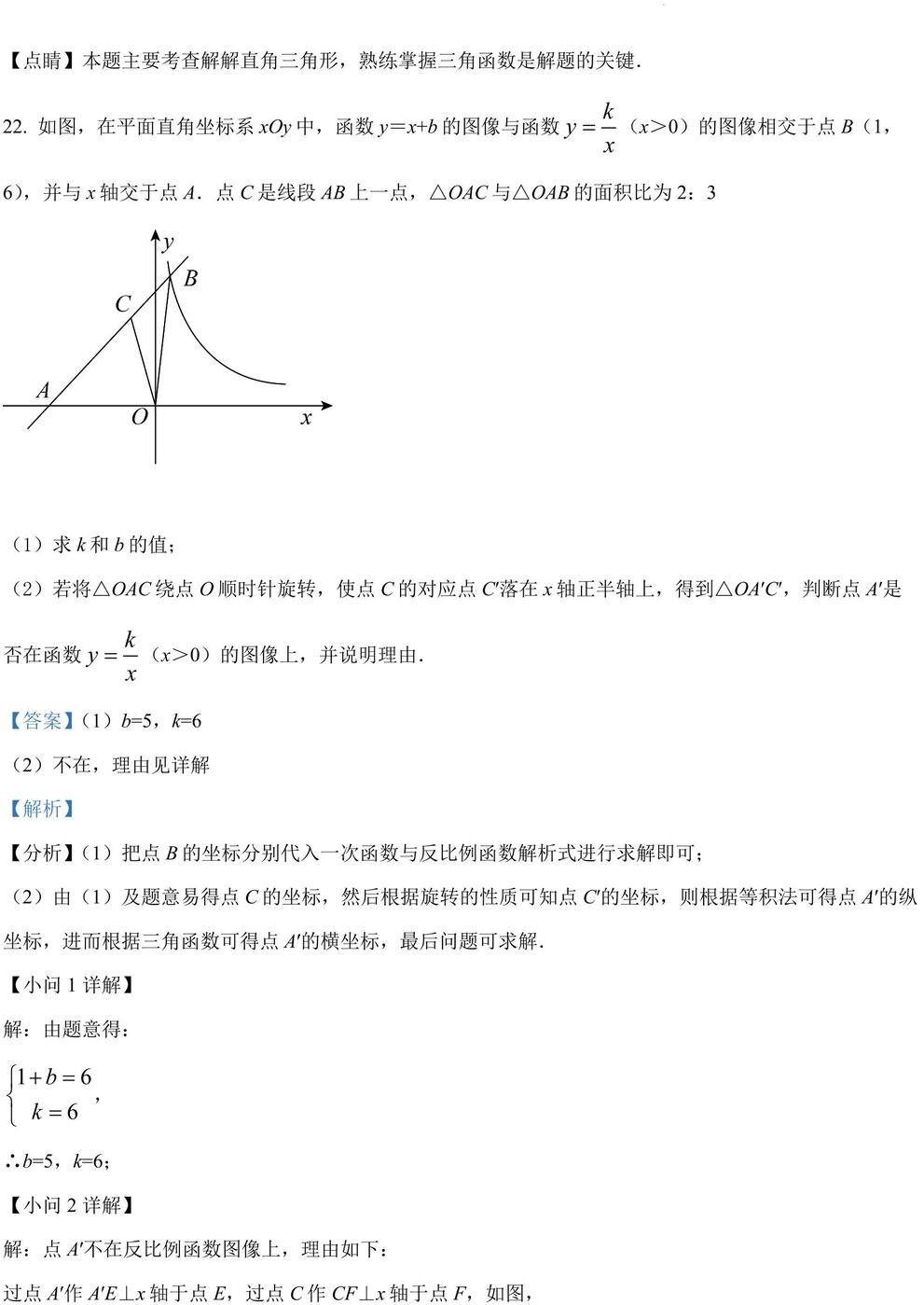
22. 如图，在平面直角坐标系 xOy中，函数 y＝x+b的图像与函数 （x＞0）的图像相交于点 B（1，
6），并与 x轴交于点 A．点 C是线段 AB上一点，△OAC与△OAB的面积比为 2：3
（1）求 k和 b的值；
（2）若将△OAC绕点 O顺时针旋转，使点 C的对应点 C′落在 x轴正半轴上，得到△OA′C′，判断点 A′是否在函数 （x＞0）的图像上，并说明理由．
【答案】（1）b=5，k=6
（2）不在，理由见详解
【分析】（1）把点 B的坐标分别代入一次函数与反比例函数解析式进行求解即可；
（2）由（1）及题意易得点 C的坐标，然后根据旋转的性质可知点 C′的坐标，则根据等积法可得点 A′的纵坐标，进而根据三角函数可得点 A′的横坐标，最后问题可求解．
【小问 1详解】 解：由题意得：
【小问 2详解】 解：点 A′不在反比例函数图像上，理由如下： 过点 A′作 A′E⊥x轴于点 E，过点 C作 CF⊥x轴于点 F，如图，