-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
故答案为： ．
【点睛】本题考查了阅读理解能力，特殊角锐角三角函数值等知识，解决问题的关键是公式的具体情景运用．
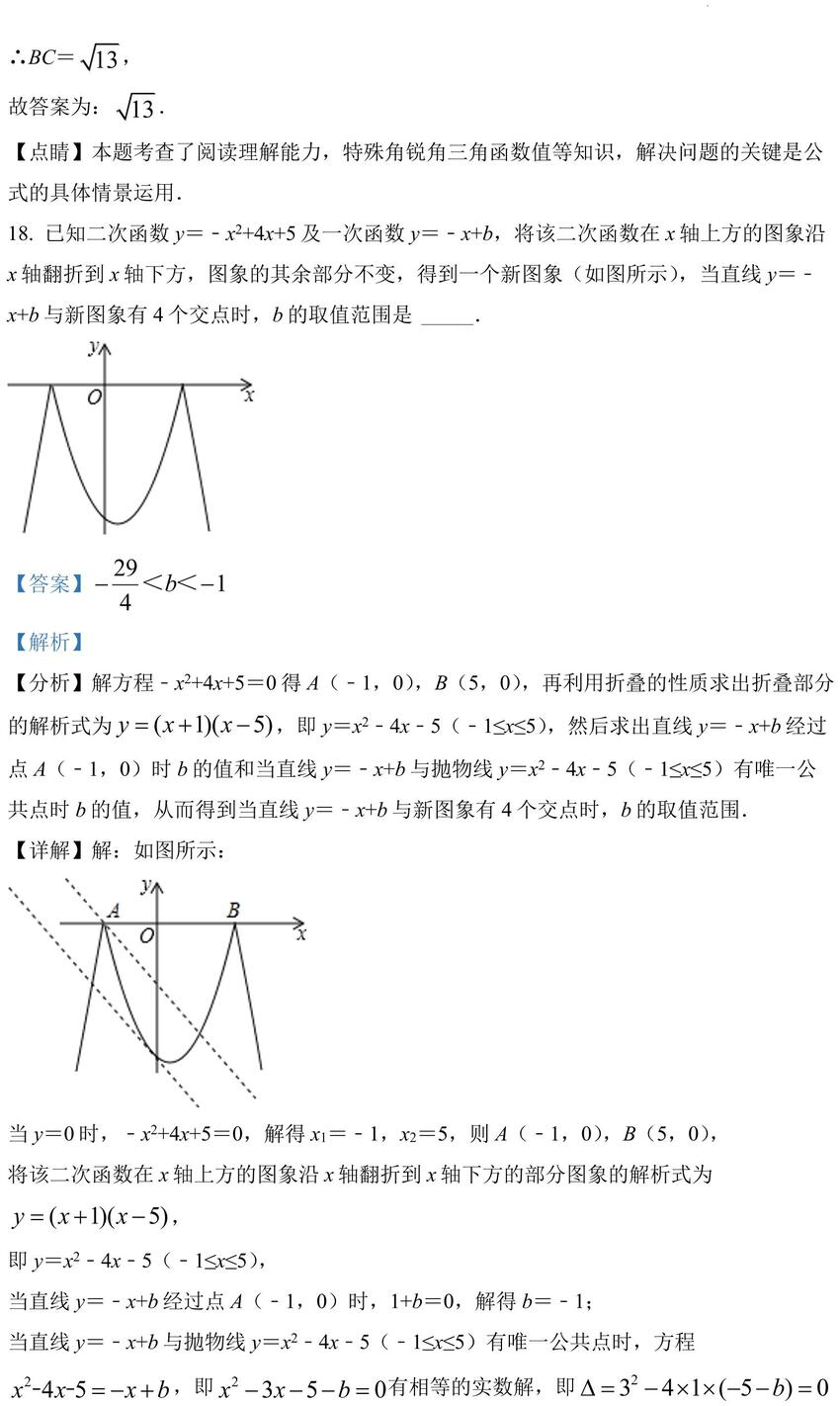
18. 已知二次函数 y＝﹣x2+4x+5及一次函数 y＝﹣x+b，将该二次函数在 x 轴上方的图象沿
x 轴翻折到 x 轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线 y＝﹣
x+b 与新图象有 4 个交点时，b 的取值范围是 _____．
【分析】解方程﹣x2+4x+5＝0得 A（﹣1，0），B（5，0），再利用折叠的性质求出折叠部分的解析式为 ，即 y＝x2﹣4x﹣5（﹣1≤x≤5），然后求出直线 y＝﹣x+b 经过点 A（﹣1，0）时 b 的值和当直线 y＝﹣x+b 与抛物线 y＝x2﹣4x﹣5（﹣1≤x≤5）有唯一公共点时 b 的值，从而得到当直线 y＝﹣x+b 与新图象有 4 个交点时，b 的取值范围．
【详解】解：如图所示： 当 y＝0 时，﹣x2+4x+5＝0，解得 x1＝﹣1，x2＝5，则 A（﹣1，0），B（5，0）， 将该二次函数在 x 轴上方的图象沿 x 轴翻折到 x 轴下方的部分图象的解析式为即 y＝x2﹣4x﹣5（﹣1≤x≤5）， 当直线 y＝﹣x+b 经过点 A（﹣1，0）时，1+b＝0，解得 b＝﹣1； 当直线 y＝﹣x+b 与抛物线 y＝x2﹣4x﹣5（﹣1≤x≤5）有唯一公共点时，方程
，即 有相等的实数解，即