-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
故答案为： ．
【点睛】本题考查了正方形性质、三角形中位线性质、折叠性质、全等三角形判定与性质、相似三角形的性质与判定、三角函数定义等知识点，找到相似三角形是解题关键．
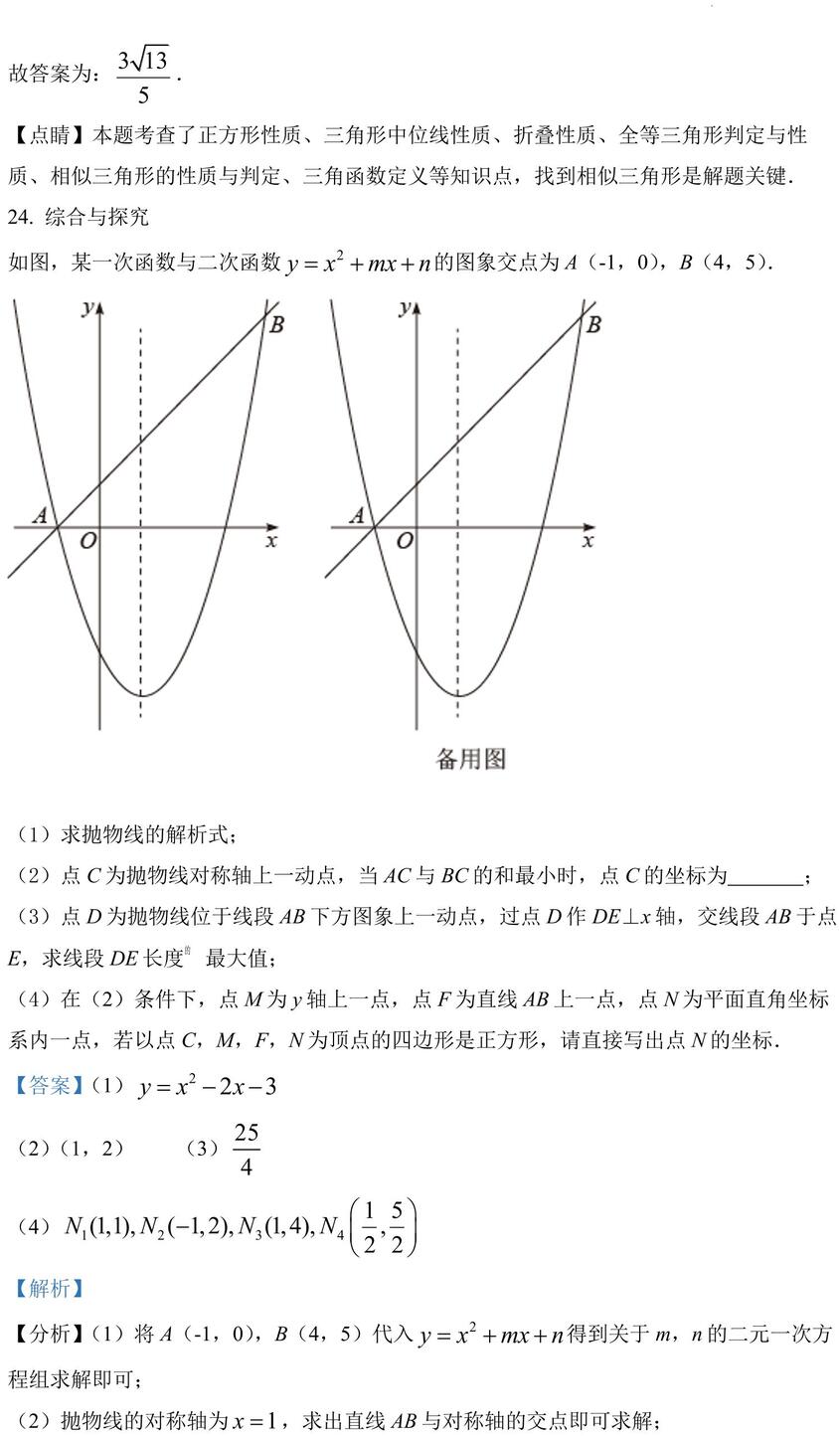
24. 综合与探究 如图，某一次函数与二次函数 的图象交点为 A（-1，0），B（4，5）．
（1）求抛物线的解析式；
（2）点 C 为抛物线对称轴上一动点，当 AC 与 BC 的和最小时，点 C 的坐标为 ；
（3）点 D 为抛物线位于线段 AB 下方图象上一动点，过点 D作 DE⊥x 轴，交线段 AB 于点
E，求线段 DE 长度 最大值；
（4）在（2）条件下，点 M 为 y 轴上一点，点 F 为直线 AB 上一点，点 N 为平面直角坐标系内一点，若以点 C，M，F，N 为顶点的四边形是正方形，请直接写出点 N 的坐标．
【答案】（1）
【分析】（1）将 A（-1，0），B（4，5）代入 得到关于 m，n 的二元一次方程组求解即可；
（2）抛物线的对称轴为 ，求出直线 AB 与对称轴的交点即可求解；