2022年黑龙江省大庆市初中学业水平考试(中考)数学试卷

对各选项逐项分析可得出正确答案．

【详解】解：A、设∠1、∠2 为锐角， 因为：∠1+∠2+∠3=180°， 所以：∠3可以为锐角、直角、钝角，所以该三角形可以是锐角三角形，也可以是直角或钝角三角形， 故 A选项不正确，符合题意；

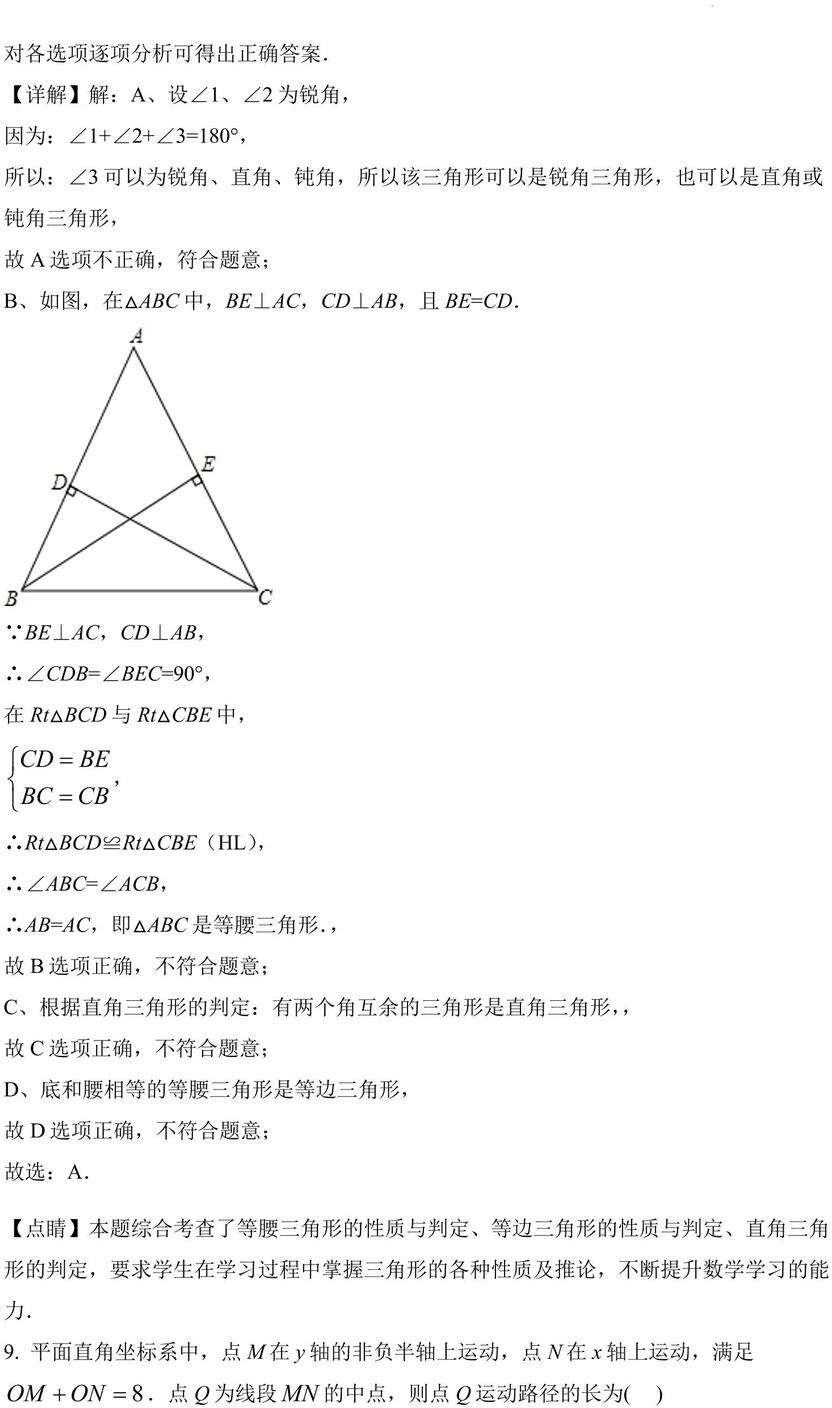
B、如图，在△ABC 中，BE⊥AC，CD⊥AB，且 BE=CD． 在 Rt△BCD 与 Rt△CBE 中，

∴AB=AC，即△ABC 是等腰三角形．， 故 B选项正确，不符合题意；

C、根据直角三角形的判定：有两个角互余的三角形是直角三角形，， 故 C选项正确，不符合题意；

D、底和腰相等的等腰三角形是等边三角形， 故 D选项正确，不符合题意； 故选：A．

【点睛】本题综合考查了等腰三角形的性质与判定、等边三角形的性质与判定、直角三角形的判定，要求学生在学习过程中掌握三角形的各种性质及推论，不断提升数学学习的能力．

9. 平面直角坐标系中，点 M 在 y 轴的非负半轴上运动，点 N 在 x 轴上运动，满足

．点 Q 为线段 的中点，则点 Q 运动路径的长为( )