-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
∴S 四边形 ABCD= ．
【点睛】本题考查等边三角形的性质，三角形全等判定与性质，正方形的性质，勾股定理，掌握等边三角形的性质，三角形全等判定与性质，正方形的性质，勾股定理是解题关键．
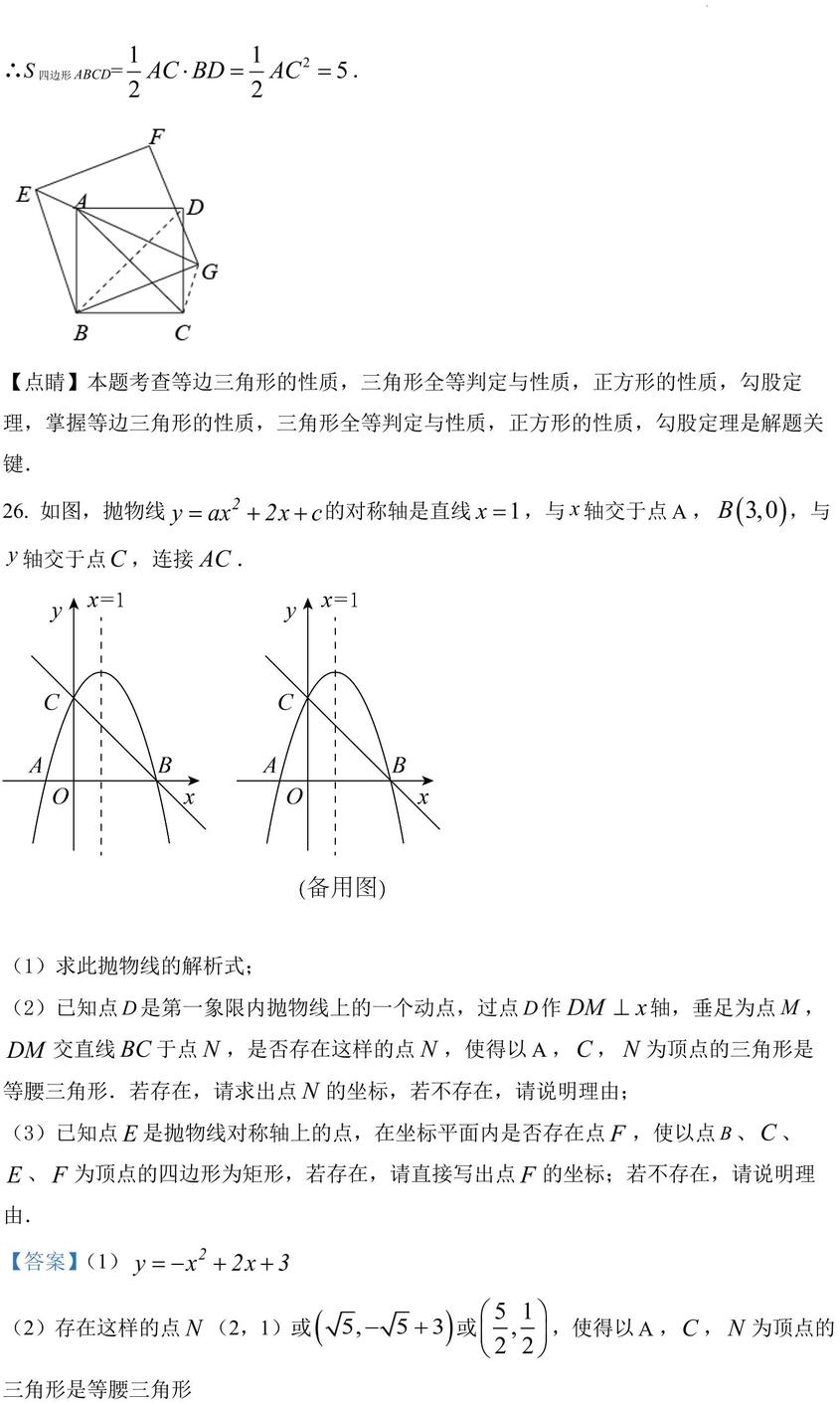
26. 如图，抛物线 的对称轴是直线 ，与 轴交于点 ， ，与轴交于点 ，连接 ．
（1）求此抛物线的解析式；
（2）已知点 是第一象限内抛物线上的一个动点，过点 作 轴，垂足为点 ，交直线 于点 ，是否存在这样的点 ，使得以 ， ， 为顶点的三角形是等腰三角形．若存在，请求出点 的坐标，若不存在，请说明理由；
（3）已知点 是抛物线对称轴上的点，在坐标平面内是否存在点 ，使以点 、 、
、 为顶点的四边形为矩形，若存在，请直接写出点 的坐标；若不存在，请说明理由．
【答案】（1）
（2）存在这样的点 （2，1）或 或 ，使得以 ， ， 为顶点的三角形是等腰三角形