-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【点睛】本题考查了切线的判定，勾股定理，等腰三角形的性质、相似三角形的性质与判定，平行线分线段成比例，解题的关键是学会添加常用辅助线，构造平行线解决问题．
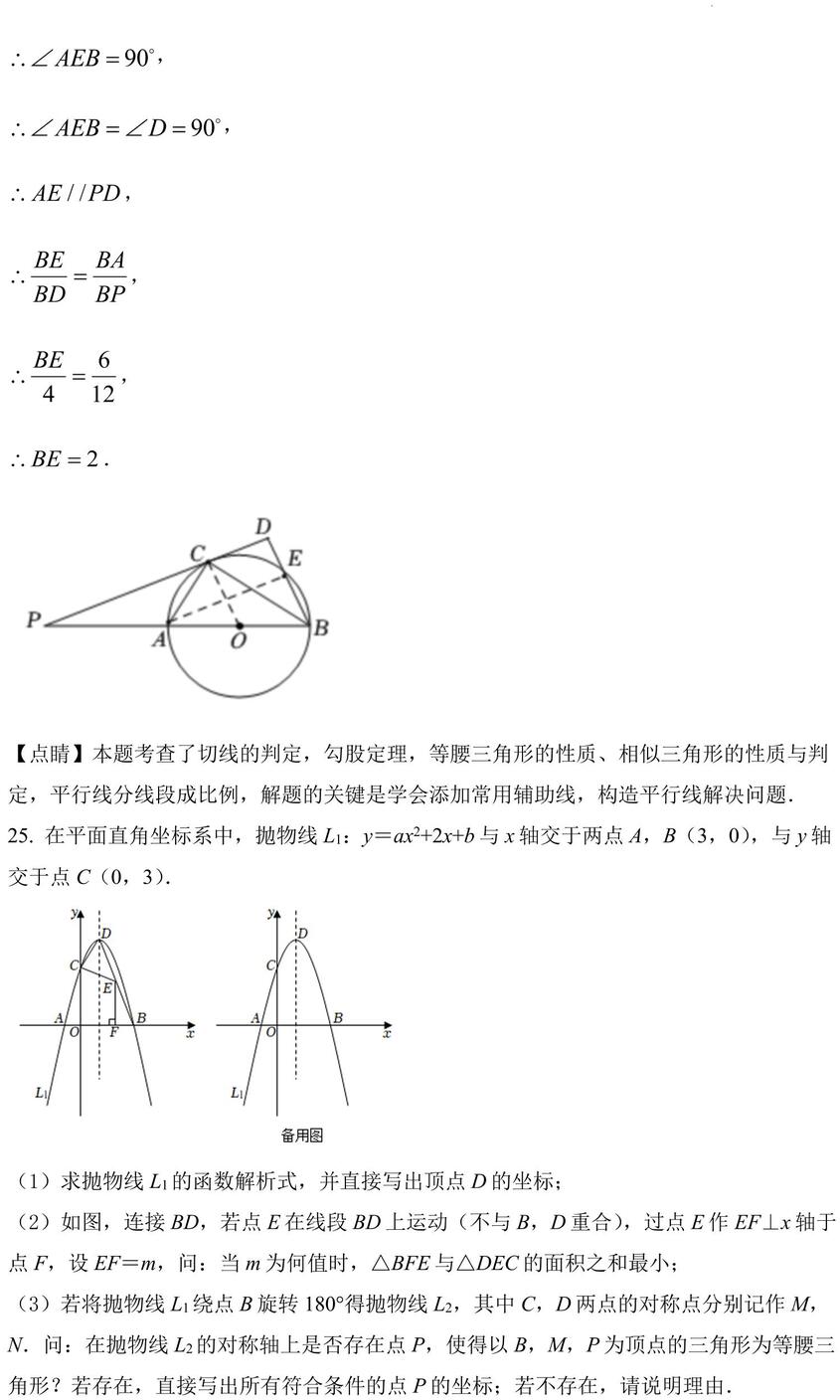
25. 在平面直角坐标系中，抛物线 L1：y＝ax2+2x+b 与 x 轴交于两点 A，B（3，0），与 y 轴交于点 C（0，3）．
（1）求抛物线 L1的函数解析式，并直接写出顶点 D 的坐标；
（2）如图，连接 BD，若点 E 在线段 BD 上运动（不与 B，D重合），过点 E 作 EF⊥x 轴于点 F，设 EF＝m，问：当 m 为何值时，△BFE 与△DEC 的面积之和最小；
（3）若将抛物线 L1绕点 B 旋转 180°得抛物线 L2，其中 C，D两点的对称点分别记作 M，
N．问：在抛物线 L2的对称轴上是否存在点 P，使得以 B，M，P 为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的点 P 的坐标；若不存在，请说明理由．