2022年广西省北部湾初中学业水平考试(中考)数学试卷

解得 ； 综上所述，当抛物线 与线段MN只有一个交点时，a 的取值范围为 或 或 ．

【点睛】本题主要考查了二次函数的综合应用，包括求二次函数与 x 轴的交点、利用二次函数解决图形问题等知识，解题关键是熟练运用数形结合和分类讨论的思想分析问题．

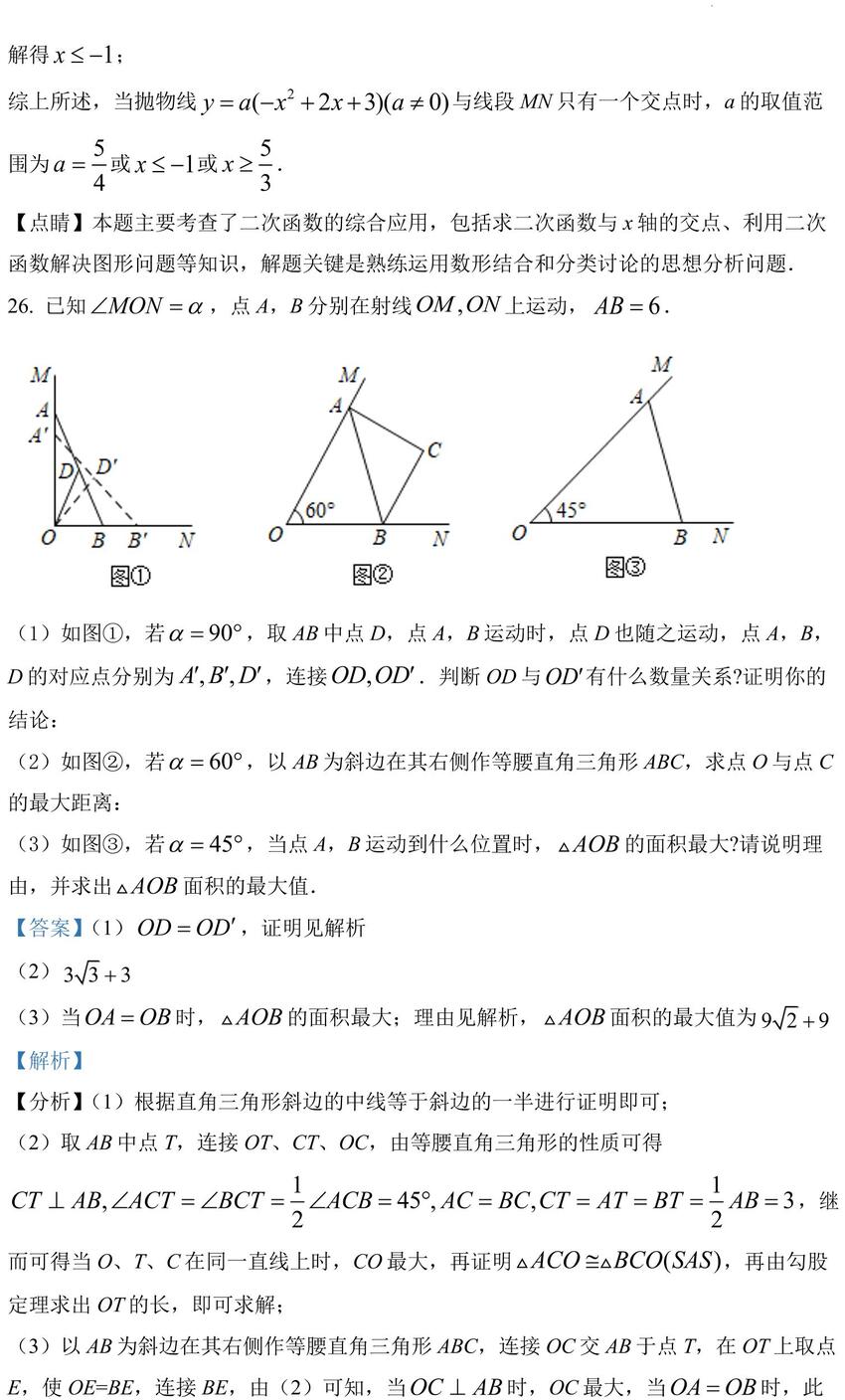
26. 已知 ，点 A，B 分别在射线 上运动， ．

（1）如图①，若 ，取 AB 中点 D，点 A，B 运动时，点 D也随之运动，点 A，B，

D 的对应点分别为 ，连接 ．判断 OD 与 有什么数量关系?证明你的结论：

（2）如图②，若 ，以 AB 为斜边在其右侧作等腰直角三角形 ABC，求点 O 与点 C的最大距离：

（3）如图③，若 ，当点 A，B 运动到什么位置时， 的面积最大?请说明理由，并求出 面积的最大值．

【答案】（1） ，证明见解析

（3）当 时， 的面积最大；理由见解析， 面积的最大值为

【分析】（1）根据直角三角形斜边的中线等于斜边的一半进行证明即可；

（2）取 AB 中点 T，连接 OT、CT、OC，由等腰直角三角形的性质可得而可得当 O、T、C 在同一直线上时，CO 最大，再证明 ，再由勾股定理求出 OT 的长，即可求解；

（3）以 AB 为斜边在其右侧作等腰直角三角形 ABC，连接 OC交 AB 于点 T，在 OT 上取点

E，使 OE=BE，连接 BE，由（2）可知，当 时，OC 最大，当 时，此