证 明 题（数学·2022年·河北省）

如图，平面直角坐标系中，线段AB的端点为A(-8,19),B(6,5).

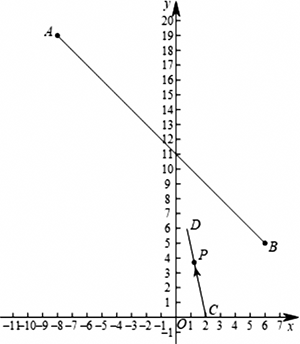
(1)求AB所在直线的解析式；

(2)某同学设计了一个动画：在函数y=mx+n(m≠0,y≥0)中，分别输入m和n的值，使得到射线CD其中C(c,0).当c=2时，会从c处弹出一个光点P，并沿CD飞行；当c≠2时，只发出射线而无光点弹出.

①若有光点P弹出，试推算m，n应满足的数量关系:

2当有光点P弹出，并击中线段AB上的整点(横、纵坐标都是整数)时，线段AB就会发光，求此时整数m的个数.

解答提示

(1)设直线AB的解析式为y=kx+b(b≠0)，把点A(-8,19),B(6,5)代入得：，解得：,∴AB所在直线的解析式为y=-x+11.(2)① n=-2m，理由如下：若有光点P弹出，则c=2，∴点C(2,0),代入y=mx+n(m≠0,y≥0)得：2m+n=0.∴若有光点P弹出，m,n满足的数量关系为n=-2m.②由①得n=-2m，∴y=mx+n=mx-2m=(x-2)m，∵点A(-8,19),B(6,5),AB所在直线的解析式为y=-x+11，∴线段AB上的其它整点为：(-7,18),(-6,17),(-5,16),(-4,15),(-3,14),(-2,13),(-1,12),(0,11),(1,10),(2,9),(3,8),(5,6),∵有光点P弹出，并击中线段AB上的整点，∴直线CD过整数点，当击中线段AB上的整点(-8,19)时，19=(-8-2)m，得m=-19/10(不合题意，舍去)，当击中线段AB上的整点(-7,18)时，18=(-7-2)m，得m=-2，当击中线段AB上的整点(-6,17)时，17=(-6-2)m，得m=-17/8(不合题意，舍去)，当击中线段AB上的整点(-...

查看完整答案，请下载word版