2010年广东省深圳市中考试题-几何-解析几何-坐标系

证明题（数学·2010年·广东省深圳市）

如图(左)所示,以点M(-1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,直线y=-/3 x-5/3与⊙M相切于点H,交x轴于点E,交y轴于点F.

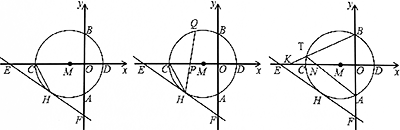
(1)请直接写出OE,⊙M的半径r，CH的长;

(2)如图(中)所示,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;

(3)如图(右)所示,点K为线段EC上一动点(不与E,C重合),连接BK交⊙M于点T,弦AT交ⅹ轴于点N.是否存在一个常数a,始终满足MN•MK=a,如果存在,请求出a的值;如果不存在,请说明理由.

解答提示

(1)如图，连接HM. ∵直线y=-/3 x-5/3中，令y=0，则x=-5，即OE=5;令x=0，则y=-5/3，故F点的坐标为(0,-5/3),∴EF==10/3,∵M(-1,0),∴EM=4,∵∠E=∠E,∠AOE=∠EHM,∴△EMH∼△EFO,∴HM/OF=EM/EF,即,∴r=2;∵CH是Rt△EMH斜边上的中线，∴CH=1/2 EM=2.(2)如图，连接DQ、CQ. ∵∠CHP=∠D,∠CPH=∠QPD,∴△CHP∼△QDP.∴CH:DQ=HP:PD=2:3,...

查看完整答案，请下载word版

几何

自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识．下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是【】

下列几何体都是由4个大小相同的小正方体组成的，其中主视图与左视图相同的几何体是【】

泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的【】

中国美食讲究色香味美，优雅的摆盘造型也会让美食锦上添花．图①中的摆盘，其形状是扇形的一部分，图②是其几何示意图（阴影部分为摆盘），通过测量得到AC=BD=12cm，C，D两点之间的距离为4cm，圆心角为60°，则图中摆盘的面积是【】

如图是一张长12cm，宽10cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分（阴影部分）可制成底面积24cm2是的有盖的长方体铁盒．则剪去的正方形的边长为cm．

如图，在RtΔABC中，∠ACB=90°，AC=3，BC=4，CD⊥AB，垂足为D，E为BC的中点，AE与CD交于点F，则DF的长为．

如图，四边形OABC是平行四边形，以点O为圆心，OC为半径的⊙O与AB相切于点B，与AO相交于点D，AO的延长线交⊙O于点E，连接EB交OC于点F，求∠C和∠E的度数．

阅读与思考下面是小宇同学的数学日记，请仔细阅读并完成相应的任务．×年×月×日星期日没有直角尺也能作出直角今天，我在书店一本书上看到下面材料：木工师傅有一块如图①所示的四边形木板，他已经在木板上画出一条裁割线AB，现根据木板的情况，要过AB上的一点C，作出AB的垂线，用锯子进行裁割，然而手头没有直角尺，怎么办呢？办法一：如图①，可利用一把有刻度的直尺在AB上量出CD=30cm，然后分别以D，C为圆心，以50cm与40cm为半径画圆弧，两弧相交于点E，作直线CE，则∠DCE必为90°．办法二：如图②，可以取一根笔直的木棒，用铅笔在木棒上点出M，N两点，然后把木棒斜放在木板上，使点M与点C重合，用铅笔在木板上将点N对应的位置标记为点Q，保持点N不动，将木棒绕点N旋转，使点M落在AB上，在木板上将点M对应的位置标记为点R．然后将RQ延长，在延长线上截取线段QS=MN，得到点S，作直线SC，则∠RCS=90°．我有如下思考：以上两种办法依据的是什么数学原理呢？我还有什么办法不用直角尺也能作出垂线呢？……任务：（1）填空；“办法一”依据的一个数学定理是；（2）根据“办法二”的操作过程，证明∠RCS=90°；（3）①尺规作图：请在图③的木板上，过点C作出AB的垂线（在木板上保留作图痕迹，不写作法）；②说明你的作法依据的数学定理或基本事实（写出一个即可）

图①是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过．图②是两圆弧翼展开时的截面图，扇形ABC和DEF是闸机的“圆弧翼”，两圆弧翼成轴对称，BC和EF均垂直于地面，扇形的圆心角∠ABC=∠DEF=28°，半径BA=ED=60cm，点A与点D在同一水平线上，且它们之间的距离为10cm．（1）求闸机通道的宽度，即BC与EF之间的距离（参考数据：sin⁡28°≈0.47，cos⁡28°≈0.88，tan⁡28°≈0.53）；（2）经实践调查，一个智能闸机的平均检票速度是一个人工检票口平均检票速度的2倍，180人的团队通过一个智能闸机口比通过一个人工检票口可节约3分钟，求一个智能闸机平均每分钟检票通过的人数．

问题情境：如图①，点E为正方形ABCD内一点，∠AEB=90°，将RtΔABE绕点B按顺时针方向旋转90°，得到ΔCBE'（点A的对应点为点C），延长AE交CE'于点F，连接DE．猜想证明：（1）试判断四边形BE' FE的形状，并说明理由；（2）如图②，若DA=DE，请猜想线段CF与FE'的数量关系并加以证明；解决问题：（3）如图①，若AB=15，CF=3，请直接写出DE的长．

解析几何

如图(1)，(2)所示，矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2.动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上)，当动点N运动到点A时，M、N两点同时停止运动.连接FM、FN，当F、N、M不在同一直线时，可得△FMN，过△FMN三边的中点作△PWQ.设动点M、N的速度都是1个单位/秒，M、N运动的时间为x秒.试解答下列问题：(1)说明△FMN∽△QWP(2)设0≤x≤4(即M从D到A运动的时间段).试问x为何值时，△PWQ为直角三角形？当x在何范围时，△PQW不为直角三角形？(3)问当x为何值时，线段MN最短？求此时MN的值.

如图，抛物线y=-5/4 x2+17/4 x+1与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C(3，0).(1)求直线AB的函数关系式;(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N.设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围;(3)设在(2)的条件下(不考虑点P与点0，点C重合的情况)，连接CM，BN，当t为何值时，四边形BCN为平行四边形?问对于所求的t值，平行四边形BCMN是否菱形?请说明理由.

如图，△OAB的顶点O(0,0)，顶点A,B分别在第一、四象限，且AB⊥x轴，若AB=6,OA=OB=5，则点A的坐标是【】

某项工作，已知每人每天完成的工作量相同，且一个人完成需12天.若m个人共同完成需n天，选取6组数对(m,n)，在坐标系中进行描点，则正确的是【】

如图，平面直角坐标系中，线段AB的端点为A(-8,19),B(6,5).(1)求AB所在直线的解析式；(2)某同学设计了一个动画：在函数y=mx+n(m≠0,y≥0)中，分别输入m和n的值，使得到射线CD其中C(c,0).当c=2时，会从c处弹出一个光点P，并沿CD飞行；当c≠2时，只发出射线而无光点弹出.①若有光点P弹出，试推算m，n应满足的数量关系:2当有光点P弹出，并击中线段AB上的整点(横、纵坐标都是整数)时，线段AB就会发光，求此时整数m的个数.

如图，点A(0,3)、B(1,0)，将线段AB平移得到线段DC，若∠ABC=90°,BC=2AB，则点D的坐标是【】

在平面直角坐标系中，点P(- 20,a) 与点Q(b,13) 关于原点对称，则a+b的值为【】

如图1，在平面直角坐标系中，正方形OABC的顶点A在x轴的正半轴上.如图2，将正方形OABC绕O逆时针旋转，旋转角为α(0°<α<45°)，AB交直线y=x于点E，BC交y轴于点F. (1)当旋转角∠EOF为多少度时，OE=OF；（直接写出结果，不要求写解答过程）；(2)若点A(4,3)，求FC的长；(3)如图3，对角线AC交y轴于点M，交直线y=x于点N，连接FN.将△OFN与△OCF的面积分别为S1,S2，设S=S1-S2,AN=n，求S关于n的函数表达式.

在平面直角坐标系中，将点(1,1)向右平移2个单位后，得到的点的坐标是【】

在平面直角坐标系中,点P(-2，-3)所在的象限是【】

坐标系

如图所示，将正方形OEFG放在平面直角坐标系中，O是坐标原点，点E的坐标为(2,3)，则点F的坐标为.

如图，在平面直角坐标系中，ΔOAB的顶点A，B的坐标分别为(3,)，(4,0).把ΔOAB沿x轴向右平移得到ΔCDE，如果点D的坐标为(6,)，则点E的坐标为.

在半面直角坐标系中，点(3,2)关于x轴对称的点的坐标为【】

如图，已知点A(5,2),B(5，4),C(8，1)，直线l⊥x轴，垂足为点M(m，0),其中m<5/2，若△A'B'C'与△ABC关于直线l对称，且△A'B'C'有两个顶点在函数y=k/x(k≠0)的图像上，则k的值为.

如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2．将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是【】

已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为【】

如图(左)所示,以点M(-1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,直线y=-/3 x-5/3与⊙M相切于点H,交x轴于点E,交y轴于点F. (1)请直接写出OE,⊙M的半径r，CH的长;(2)如图(中)所示,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;(3)如图(右)所示,点K为线段EC上一动点(不与E,C重合),连接BK交⊙M于点T,弦AT交ⅹ轴于点N.是否存在一个常数a,始终满足MN•MK=a,如果存在,请求出a的值;如果不存在,请说明理由.

已知点P(a+1,2a-3)关于x轴的对称点在第一象限，则a的取值范围是【】

抛物线y=x2-1交x轴于A,B两点(A在B的左边),(1) ▱ACDE的顶点C在y轴的正半轴上，顶点E在y轴右侧的抛物线上.①如图(1)，若点C的坐标是(0,3)，点E的横坐标是5，直接写出点A,D的坐标;②如图(2)，若点D在抛物线上，且▱ACDE的面积是12，求点E的坐标.(2)如图(3)，F是原点O关于抛物线顶点的对称点，不平行y轴的直线l分别交线段AF,BF(不含端点)于G,H两点.若直线l与抛物线只有一个公共点，求证：FG+FH的值是定值.

在平面直角坐标系xOy中，点M(-4，2)关于x轴对称的点的坐标是【】