如图,正方形ABCD的边长为a,点E在AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF=√2 BE,CF与AD相交于点G,连接EC,EF,EG,则下列结论:
①∠ECF=45°;②△AEG的周长为(1+√2/2)a;③BE²+DG²=EG²;④△EFA的面积的最大值为1/8 a².
其中,正确的结论是______.(只填序号)
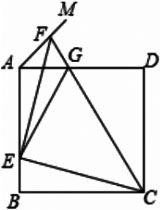
如图,正方形ABCD的边长为a,点E在AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF=√2 BE,CF与AD相交于点G,连接EC,EF,EG,则下列结论:
①∠ECF=45°;②△AEG的周长为(1+√2/2)a;③BE²+DG²=EG²;④△EFA的面积的最大值为1/8 a².
其中,正确的结论是______.(只填序号)

①④
【解析】
解答过程见word版
如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.
如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△ADE≌△CED;(2)求证:△DEF是等腰三角形.
如图,B是AD的中点,BC//DE,BC=DE.求证:∠C=E.
如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE,求证:△ABD≌△ACE.
如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°,求∠BCA的度数.
如图,D是AB上一点,DF交AC于点E,DE=EF,FC∥AB,求证:△ADE≌△CEF.
已知:如图,E、F在AC上,AD//CB且AD=CB,∠D=∠B.求证:AE=CF.
如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.(1)求证:△AOC≌△BOD;(2)若AD=1,BD=2,求CD的长.
边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为________.
如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF,若AB=2,则OF的长度为【 】
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求BG的长.
如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为【 】
如图,在正方形ABCD中,点P从点A出发,沿正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x形成的函数关系图像大致是【 】
完全相同的4个正方形面积之和是 100,则正方形的边长是【 】
如图所示,四边形 ABCD,DEFG,GHIJ 均为正方形,且SABCD=10,SGHI=1,则正方形 DEFG 的边长可以是________(写出一个答案即可).
如图,正方形ABCD的边长为4,点E在边BC上,且BE=1,F为对角线BD上一动点,连接CF,则CF+EF的最小值为______.