如图,在菱形ABCD中,∠C=120°,点E在射线BC上运动(不与点B,C重合),△AEB关于AE的轴对称图形为△AEF.
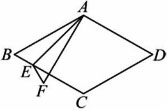
(1)当∠BAF=30°时,试判断线段AF和线段AD的数量和位置关系,并说明理由;
(2)若AB=6+6√3,⨀O是△AEF的外接圆,设⨀O的半径为r,
①求r的取值范围;
②连接FD,直线FD能否与⨀O相切?如果能,求BE的长度;如果不能,请说明理由.
如图,在菱形ABCD中,∠C=120°,点E在射线BC上运动(不与点B,C重合),△AEB关于AE的轴对称图形为△AEF.

(1)当∠BAF=30°时,试判断线段AF和线段AD的数量和位置关系,并说明理由;
(2)若AB=6+6√3,⨀O是△AEF的外接圆,设⨀O的半径为r,
①求r的取值范围;
②连接FD,直线FD能否与⨀O相切?如果能,求BE的长度;如果不能,请说明理由.
解答过程见word版
如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线垂直,垂足为D.连接并延长BC,交AD的延长线于点E.(1)求证:AE=AB;(2)若AB=10,BC=6,求CD的长.
已知△ABE为直角三角形,∠ABE=90°,BC为圆O的切线,C为切点,CA=CD,则△ABC和△CDE的面积之比为【 】
如图,AB为⊙O的直径,直线 CD与⊙O 相切于点 C,连接AC,若∠ACD=50°,则∠BAC 的度数为【 】
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.
如图,点P是四边形ABCD外接圆⊙O上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD,连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF=________.